A Neat Radical Equation Relating The Radii Of Three Circles Tangent To

A Neat Radical Equation Relating The Radii Of Three Circles Tangent To In this video, i showed how to derive the equation 1 sqrt(c) = 1 sqrt(a) 1 sqrt(b) which relates the radii of three circles externally tangent to one anoth. At first join the centers of the circles to get a big triangle with known sides. first calculate the sides of triangle . a=r1 r2. b=r2 r3. c=r3 r1 [here r1,r2,r3 are radii of the above three triangles] now calculate half perimeter to calculate the area of large triangle : s=(a b c) 2. area of big triangle is :.

Prove An Equation On Radii Of 3 Tangent Circles Geometry Three circles with radii 1, 2, and 3 ft. are externally tangent to one another, as shown in the figure. find the area of the sector of the circle of radius 1 ft. that is cut off by the line segments joining the center of that circle to the centers of the other two circles. the length of the sides of a triangle is calculated by the sum of the. Tangent circles. download wolfram notebook. two circles with centers at with radii for are mutually tangent if. (1) if the center of the second circle is inside the first, then the and signs both correspond to internally tangent circles. if the center of the second circle is outside the first, then the sign corresponds to externally tangent. Let the centers of the circles form the triangle and let its side lengths be , , . using conway triangle notation, define,,. half the triangle's area is then given by. in those terms, suppose the cartesian coordinates of three centers are at , , and the corresponding radii are , , . then the radical circle of the three circles , , is the circle. Example 6: tangents to the radical axis of a pair of circles the radical axis of a pair of circles is the line joining the points of intersection. the lengths of tangents from a given point on this axis to the two circles are the same. d f g b a h e c ⇒ a4 4·a2·b2 2·a2·r2 r4 s4 s2· 2·a2 2·r2 2·a ⇒ a4 4·a2·b2 2·a2·r2 r4 s4 s2.
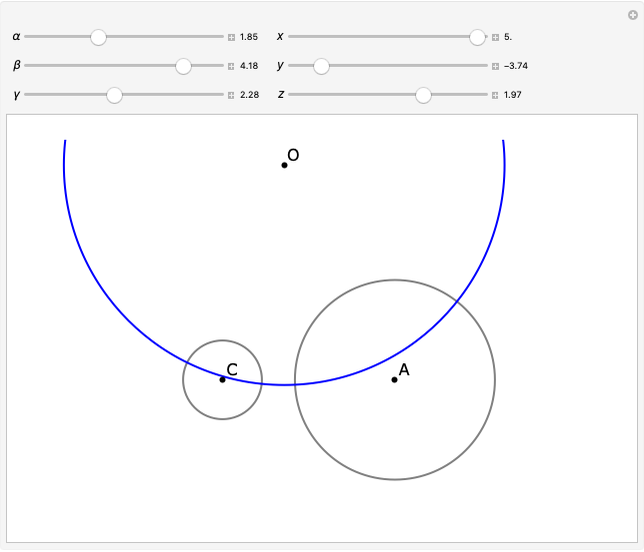
Radical Circle Of Three Circles Wolfram Demonstrations Project Let the centers of the circles form the triangle and let its side lengths be , , . using conway triangle notation, define,,. half the triangle's area is then given by. in those terms, suppose the cartesian coordinates of three centers are at , , and the corresponding radii are , , . then the radical circle of the three circles , , is the circle. Example 6: tangents to the radical axis of a pair of circles the radical axis of a pair of circles is the line joining the points of intersection. the lengths of tangents from a given point on this axis to the two circles are the same. d f g b a h e c ⇒ a4 4·a2·b2 2·a2·r2 r4 s4 s2· 2·a2 2·r2 2·a ⇒ a4 4·a2·b2 2·a2·r2 r4 s4 s2. Descartes' circle theorem (a.k.a. the kissing circle theorem) provides a quadratic equation satisfied by the radii of four mutually tangent circles. by solving this equation, one can determine the possible values for the radius of a fourth circle tangent to three given, mutually tangent circles. the theorem was first stated in a 1643 letter from rené descartes to princess elizabeth of. Three angles are 50.48^o,58.99^o and 70.53^o. three circles with radii 4, 5 and 6 form a triangle, whose sides are sum of their radii in pairs. hence sides of triangle are 4 5, 4 6 and 5 6, i.e. 9, 10 and 11.

The Radical Circle Of The Three Given Circles With The Circles L1 And Descartes' circle theorem (a.k.a. the kissing circle theorem) provides a quadratic equation satisfied by the radii of four mutually tangent circles. by solving this equation, one can determine the possible values for the radius of a fourth circle tangent to three given, mutually tangent circles. the theorem was first stated in a 1643 letter from rené descartes to princess elizabeth of. Three angles are 50.48^o,58.99^o and 70.53^o. three circles with radii 4, 5 and 6 form a triangle, whose sides are sum of their radii in pairs. hence sides of triangle are 4 5, 4 6 and 5 6, i.e. 9, 10 and 11.

Radical Circle Of Three Circles Wolfram Demonstrations Project
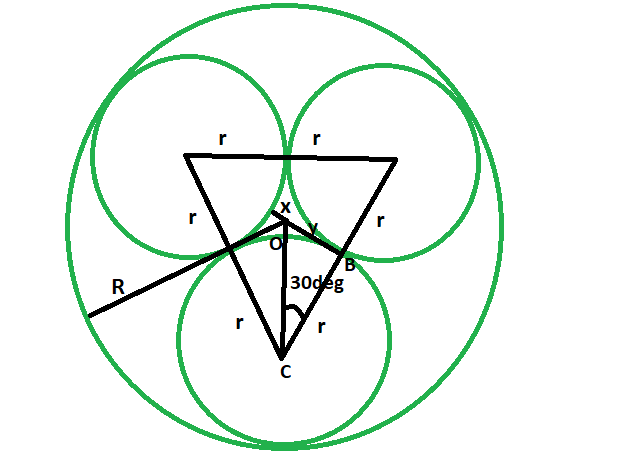
Radii Of The Three Tangent Circles Of Equal Radius Which Are Inscribed

Comments are closed.