A Square Inscribed In A Triangle2 3 5 2023
Inscribed Square In A Triangle Math Central A tricky exam question with the step by step solution. Solution 3 (similar triangles) let the center of the circle be , and the radius of the circle be . since is a rhombus with diagonals and , its area is . since and are diameters of the circle, and are right triangles. let and be the foot of the altitudes to and , respectively.
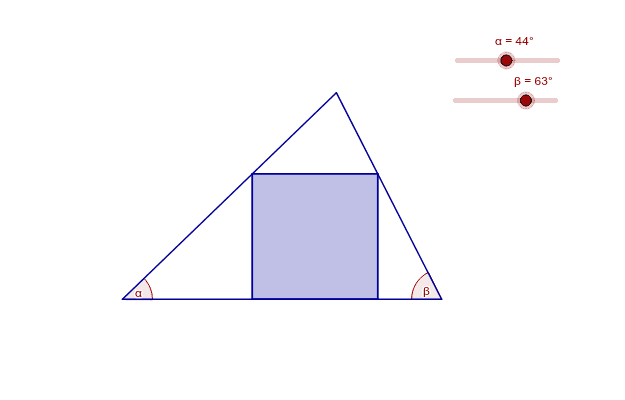
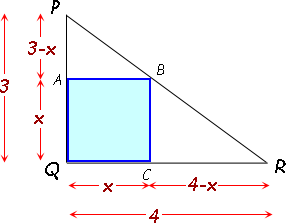
Square Inscribed In Triangle Geogebra What is the area of the square? thanks to papa in india for the suggestion!this puzzle is half of of problem 21 in the 2017 amc 10a. artofproblemsolvi. We find the area of a square inscribed in a 3 4 5 triangle. this is a pretty straightforward solution, and if you've taken a geometry class, you have all of. Because abc is a 3 4 5 triangle, it is a right triangle. consequently, triangles abc, pbs, src, and aqp are similar triangles. in each triangle, the longer leg to the shorter leg has a ratio of 4 3 (and the shorter leg to longer leg is a ratio of 3 4). suppose the square has a side length equal to s. then qr = s. A square is inscribed into a right angled triangle with length sides 3, 4 and 5 so that it lies along both legs and just touches the hypotenuse. find the length of the square. x = side of the square area of the 3 4 5 triangle is 6 sq units. area of the square is x^2 sq units. area of the smaller triangle on the side of 3 units is x*(3 x) 2.
Square Inscribed In A Triangle Geogebra Because abc is a 3 4 5 triangle, it is a right triangle. consequently, triangles abc, pbs, src, and aqp are similar triangles. in each triangle, the longer leg to the shorter leg has a ratio of 4 3 (and the shorter leg to longer leg is a ratio of 3 4). suppose the square has a side length equal to s. then qr = s. A square is inscribed into a right angled triangle with length sides 3, 4 and 5 so that it lies along both legs and just touches the hypotenuse. find the length of the square. x = side of the square area of the 3 4 5 triangle is 6 sq units. area of the square is x^2 sq units. area of the smaller triangle on the side of 3 units is x*(3 x) 2. A square is inscribed in a right triangle, as shown below. the legs of the triangle are 2 and 3. find the side length of the square. 4. reflect the triangle across its legs ab a b and bc b c. because ab = bc = 2 a b = b c = 2, the resulting figure is a square. moreover, since the inscribed yellow shape is also a square, it is easy to see that their reflections must form a central square that is congruent, and in fact, the entire figure consists of 9 9 congruent squares.

Square Inscribed In A Right Triangle Geometry Video Youtube A square is inscribed in a right triangle, as shown below. the legs of the triangle are 2 and 3. find the side length of the square. 4. reflect the triangle across its legs ab a b and bc b c. because ab = bc = 2 a b = b c = 2, the resulting figure is a square. moreover, since the inscribed yellow shape is also a square, it is easy to see that their reflections must form a central square that is congruent, and in fact, the entire figure consists of 9 9 congruent squares.

Area Of Square Inscribed In A Triangle Youtube

Geometry When Square Is Inscribed How To Identify The Similar

Comments are closed.