A Square Is Inscribed In A Circle With Radius 5 What Is The Area Of The Square

By viagraultimate On Nov 11, 2024 Last updated

Square Inside A Circle Area How to solve a geometry word problem inscribed square circle. learn more math at tcmathacademy . tabletclass math academy tcmathacademy. Here, it is very easy the 4 irregular shapes are all the same size (from symmetry). the sum of their areas is the difference between the area of the circle and the area of the square. so the shaded area is a shaded = (a circle a square) 4. if we have the side of the square, a, we get a shaded = (a circle a square) 4= (π·a 2 2 a 2) 4.

Square Inside A Circle Area If we have a square circumscribed about a circle with side 10 cm, then we can find the largest circle inscribed in the square as follows: the largest circle inscribed in a square of side s will have a radius of s 2. so for a square of side 10 cm, the largest circle in it will have a radius of 5 cm. the area of the circle will be 78.54 cm². Area of square inside a circle a = 2 r 2. where r is the radius of the circle, and also the distance from the center of the square to one of its corners. finding the area of the circle that is not inside the square (the part of the circle shaded green below). the formula for the area of a circle is a = π r 2. Calculation formula. to calculate the square in a circle, the formula is quite simple. you just need the radius (r) of the circle. here it is in all its glory: area of square = 2 * r^2. Find formulas for the square’s side length, diagonal length, perimeter and area, in terms of 'r', the inscribed circle's radius. strategy. in solving the similar problem of a square is inscribed in a circle, the key insight was that the diagonal of the square is the diameter of the circle.

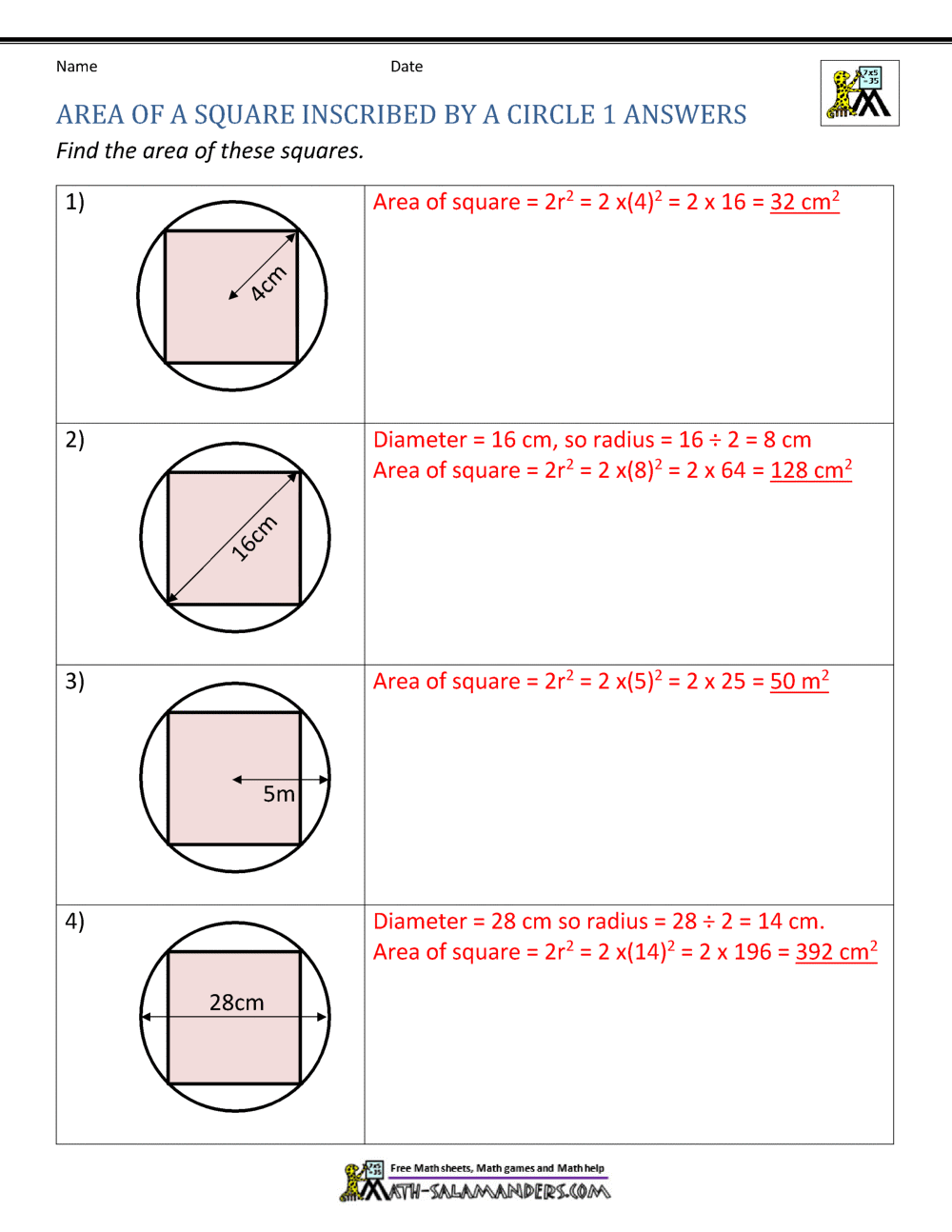
Square Inside A Circle Area Calculation formula. to calculate the square in a circle, the formula is quite simple. you just need the radius (r) of the circle. here it is in all its glory: area of square = 2 * r^2. Find formulas for the square’s side length, diagonal length, perimeter and area, in terms of 'r', the inscribed circle's radius. strategy. in solving the similar problem of a square is inscribed in a circle, the key insight was that the diagonal of the square is the diameter of the circle. Square inscribed in a circle with radius 2 in. step 1: if the diameter or the radius of the circle is known, find the length of the diagonal of the square using the fact that the diameter of the. Since the circle is inscribed in the square, the diameter of the circle equals the side length of the square diameter = 2 * radius = 2 * 5 = 10 so, the side length of the square = 10. calculate the area of the square area of the square = side length² = 10² = 100. find the difference between the area of the square and the area of the circle.

Embrace Your Unique Style and Fashion Identity: Stay ahead of the fashion curve with our A Square Is Inscribed In A Circle With Radius 5 What Is The Area Of The Square articles. From trend reports to style guides, we'll empower you to express your individuality through fashion, leaving a lasting impression wherever you go.

A square is inscribed in a circle with radius = 5, what is the area of the square?

A square is inscribed in a circle with radius = 5, what is the area of the square? A square is inscribed in a circle with radius = 4, what is the area of the square? Square Inscribed in a Circle A circle with an inscribed square – can you find the area of the square? Geometry! What is the radius of a circle inscribed in a square?? What Percentage of the Shape is Shaded - Square Inscribed in Circle A square is inscribed in a circle with radius, what is the area of the square Geometry! What is the area of a square inscribed in a quarter circle?? How to find the area of intersection between two circles using double integration Geometry! What is the area of the square inscribed in a 3-4-5 triangle?? SAT Math Challenge 01 A square is inscribed in a circle with radius 62 inches. What is the perimeter In the figure above, a square is inscribed in a ci Find the Area of Square Inscribed in a Circle of 154 cm square How to compare area of circle and inscribe square 365. If a square is inscribed in a circle then find the ratio of area square to area of circle Area of Square inscribed in a quarter circle An equilateral triangle and a square inscribed in a circle. Video inspired by Edwin Wallace. The area and perimeter of a square inscribed in a circle But why is a sphere's surface area four times its shadow? Area Ratio of Square Inscribed in a Semicircle | Geometry

Conclusion

Upon a thorough analysis, it becomes apparent that the post presents pertinent facts pertaining to A Square Is Inscribed In A Circle With Radius 5 What Is The Area Of The Square. In the full scope of the article, the creator reveals considerable expertise pertaining to the theme. Particularly, the chapter on X stands out as extremely valuable. Besides, the write-up stands out in breaking down complex concepts in an straightforward manner. What’s more, the reporter provides real-life scenarios that make the information more relatable. A further characteristic that makes this manuscript distinctive is the comprehensive analysis of an array of aspects related to A Square Is Inscribed In A Circle With Radius 5 What Is The Area Of The Square. The writers detailed technique assures that readers acquire a full grasp of the subject matter. Thanks for spending time on this publication. Should you require additional details, dont think twice to reach out to me employing email. I am ready for your responses. In wrapping up, for additional information, here are a collection of associated documents that may prove interesting:Enjoy your reading!