An Equilateral Triangle Abc Is Inscribed In A Circle Of Radius R Units

An Equilateral Triangle Abc Is Inscribed In A Circle Of Radius R Units An equilateral triangle abc of side x units is inscribed in a circle which is centered at o, as shown below. then the radius of this circle is then the radius of this circle is q. Konstantinos michailidis. nov 22, 2015. let abc equatorial triangle inscribed in the circle with radius r. applying law of sine to the triangle obc, we get. a sin60 = r sin30 ⇒ a = r ⋅ sin60 sin30 ⇒ a = √3 ⋅ r. now the area of the inscribed triangle is. a = 1 2 ⋅ am ⋅ bc. now am = ao om = r r ⋅ sin30 = 3 2 ⋅ r. and bc = a.

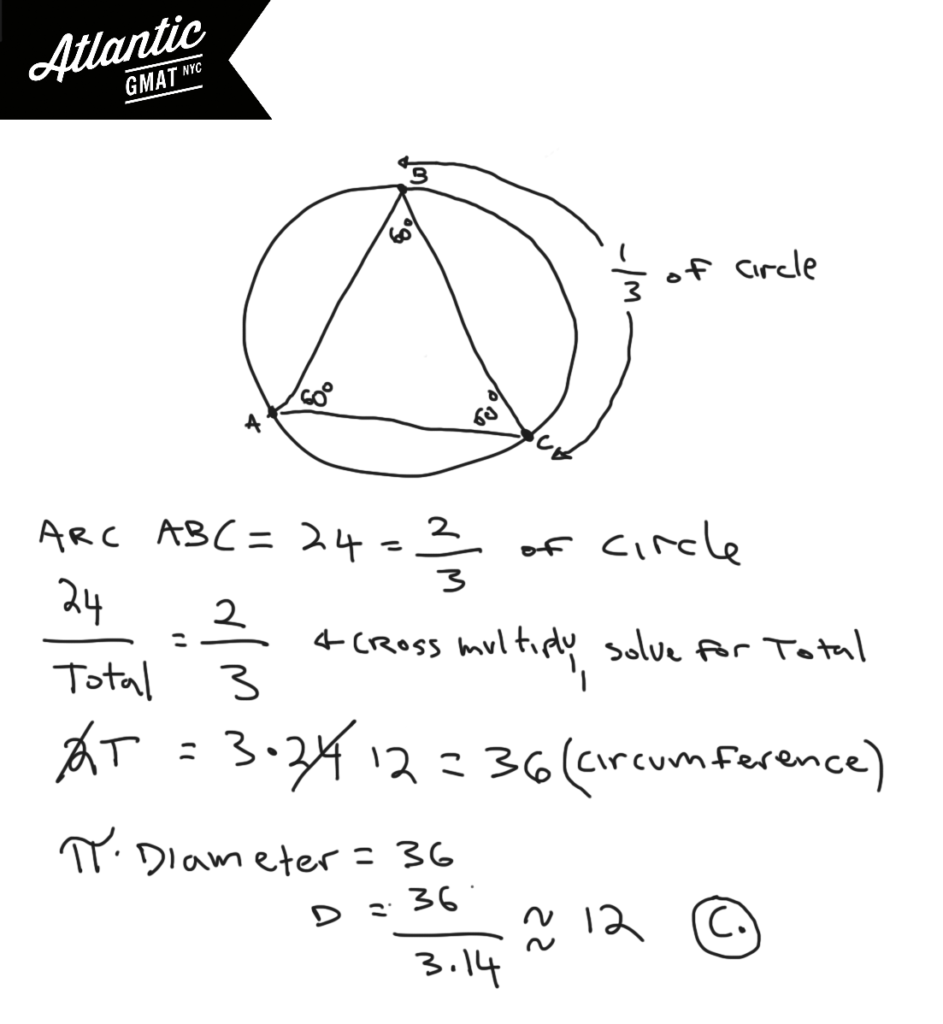
In The Figure Above Equilateral Triangle Abc Is Inscribed In The In an equilateral triangle, the radius of the circumscribed circle is equal to the side length divided by √3; calculate the radius: r = 6 √3 = 2√3 cm; area of a circle = πr^2; substitute the radius into the formula: area = π(2√3)^2 = 12π cm^2. Theorem 2.5. for any triangle abc, the radius r of its circumscribed circle is given by: 2r = a sina = b sinb = c sinc. note: for a circle of diameter 1, this means a = sina, b = sinb, and c = sin c.) to prove this, let o be the center of the circumscribed circle for a triangle abc. You can easily find the perimeter of an equilateral triangle by adding all triangles sides together. this regular triangle has all sides equal, so the formula for the perimeter is: perimeter = 3 × a. how to find the radius of the circle circumscribing the three vertices and the inscribed circle radius? circumcircle radius = 2 × h 3 = a ×. The area of an equilateral triangle is calculated using the formula a = (√3 4) s^2, where s is the length of one side. in this case, the side length of the triangle is also 6 cm, so the area of the triangle is a = (√3 4) (6 cm)^2. substituting in the values, we get: area of circle = π (6 cm)^2 = 36π cm^2.

Formulas Radius Of Inscribed And Circumscribed Circle In A Triangle You can easily find the perimeter of an equilateral triangle by adding all triangles sides together. this regular triangle has all sides equal, so the formula for the perimeter is: perimeter = 3 × a. how to find the radius of the circle circumscribing the three vertices and the inscribed circle radius? circumcircle radius = 2 × h 3 = a ×. The area of an equilateral triangle is calculated using the formula a = (√3 4) s^2, where s is the length of one side. in this case, the side length of the triangle is also 6 cm, so the area of the triangle is a = (√3 4) (6 cm)^2. substituting in the values, we get: area of circle = π (6 cm)^2 = 36π cm^2. We can use the properties of an equilateral triangle and a 30 60 90 right triangle to find the area of a circle inside an equilateral triangle, using only the triangle's side length. problem. an equilateral triangle has side length x. find the circle's area in terms of x. strategy. Equilateral triangle. this online calculator calculates characteristics of the equilateral triangle: the length of the sides, the area, the perimeter, the radius of the circumscribed circle, the radius of the inscribed circle, the altitude (height) from single known value. in geometry, an equilateral triangle is a triangle in which all three.