Area Of An Equilateral Triangle Formula Examples Definition

Area Of An Equilateral Triangle Formula Examples Definition Let’s plug in the value of the area then solve for the side: learn the method for calculating the area of an equilateral triangle using the formula area = (√3 4)s^2, where 's' denotes the side length of the equilateral triangle. keep in mind that all sides of an equilateral triangle are of equal length. As per formula: perimeter of the equilateral triangle = 3a, where “a” is the side of the equilateral triangle. step 1: find the side of an equilateral triangle using perimeter. 3a = 12. a = 4. thus, the length of side is 4 cm. step 2: find the area of an equilateral triangle using formula. area, a = √3 a 2 4 sq units.

Area Of An Equilateral Triangle Formula Examples Definition Examples on area of equilateral triangle. example 1: find the area of an equilateral triangle of side 9 cm. solution: the formula for the area of an equilateral triangle is given as, area = √ (3) 4 × (side) 2. by substituting the value of side length in the above formula, we get, = √ (3) 4 × 9 2. = 35.07 inches 2. Area of an equilateral triangle can also be calculated if the perimeter is known. perimeter of an equilateral triangle is 3a. find the side using this formula and substitute in the formula: area $= \frac{\sqrt{3}a^2}{4}$ solved examples on area of equilateral triangle. 1. find the area of an equilateral triangle whose perimeter is 12 inches. The formula for calculating the area of an equilateral triangle is elegantly simple: area=34×side2area=43×2. here, the side refers to the length of one of the triangle’s equal sides. this formula, derived using pythagoras’ theorem and trigonometry, perfectly encapsulates the symmetry of the equilateral triangle. Solution: area of equilateral triangle = √3a 2 4, where a is the side. given, a = 20 inches. therefore, area = √3×20×20 4. area of an equilateral triangle = 100√3 square inches. example 2: what is the perimeter of an equilateral triangle whose sides are 40 inches. also, find the height of an equilateral triangle.

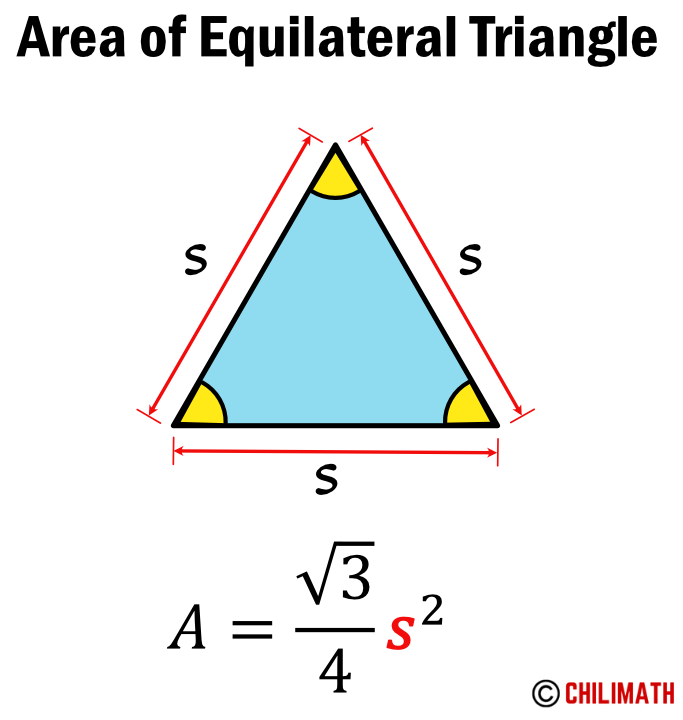
Area Of Equilateral Triangle Derivation Formula Examples Chilimath The formula for calculating the area of an equilateral triangle is elegantly simple: area=34×side2area=43×2. here, the side refers to the length of one of the triangle’s equal sides. this formula, derived using pythagoras’ theorem and trigonometry, perfectly encapsulates the symmetry of the equilateral triangle. Solution: area of equilateral triangle = √3a 2 4, where a is the side. given, a = 20 inches. therefore, area = √3×20×20 4. area of an equilateral triangle = 100√3 square inches. example 2: what is the perimeter of an equilateral triangle whose sides are 40 inches. also, find the height of an equilateral triangle. Example 2. now try it in reverse. say that an equilateral triangle has an area of {eq}12\sqrt3 { eq} and calculate the length of its sides. set the area formula equal to {eq}12\sqrt3 { eq}. Consider an equilateral triangle with side length ‘a’. draw a perpendicular bisector of a side and name the perpendicular, also called the height of the triangle, length as ‘h’. now we use the formula for the area of a triangle: area of triangle abc = \ (\frac {1} {2}\) x base x height. = \ (\frac {1} {2}\) x a x h.

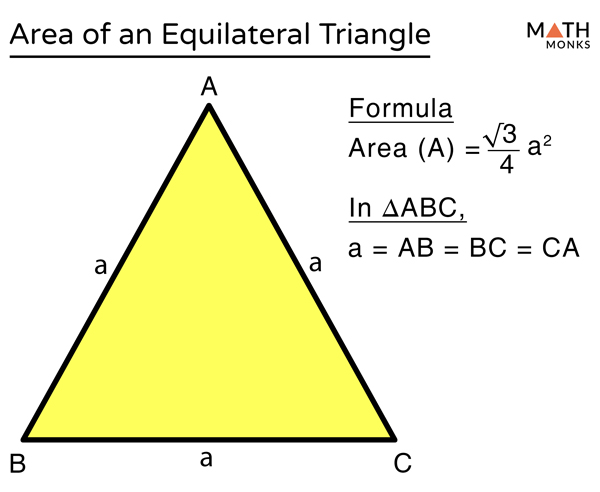
Equilateral Triangle Definition Properties Formulas Example 2. now try it in reverse. say that an equilateral triangle has an area of {eq}12\sqrt3 { eq} and calculate the length of its sides. set the area formula equal to {eq}12\sqrt3 { eq}. Consider an equilateral triangle with side length ‘a’. draw a perpendicular bisector of a side and name the perpendicular, also called the height of the triangle, length as ‘h’. now we use the formula for the area of a triangle: area of triangle abc = \ (\frac {1} {2}\) x base x height. = \ (\frac {1} {2}\) x a x h.

Area Of An Equilateral Triangle Formula Examples Definition

Formula For The Area Of An Equilateral Triangle Dewwool