Area Of Square Inscribed In A Triangle R Gmat

Geometry Area Of Square Inscribed In A Triangle Gre Gmat Cat Sat The sides of the 30 60 90 triangles become ½r : (r√3) 2 : r respectively the side of the equilateral triangle becomes 2*(r√3) 2 = r√3. if given the area of the square, we should be able to derive essentially any other information. area of an equilateral triangle. the area of an equilateral triangle equals (s²√3) 4. memorize this. 54k subscribers in the gmat community. this subreddit is for discussion of the gmat (graduate management admission test). if you're studying for the….

Area Of Square Inscribed In A Triangle Youtube 1. answer c. use tan60 to get side of triangle if you are assuming square side to be x. so side of equi. triangle is. x 2*x tan60. now ratio of area=area of square (side x) area of triangle (x 2*x tan60).after calculation and rationalisation we will get ans.c. posted from my mobile device. lacktutor. Defg (shaded) is a square inscribed in Δabc. ap is the altitude of the triangle. if ap=4, bp=5 and pc=3 what is the area of square defg? a) 125 16b) 64 9c). Half of an equilateral triangle (aep) is 30 60 90 triangle, and sides are in the ratio of a:a√3:2a. a=x 2 (half of the side of the equilateral triangle) ap=√3x 2. since it is inscribed circle, centriod and the center of the circle will be same. ap will be median, and centroid will divide it in 2:1 (2y:1y) 3y=ap=√3x 2. First calculate the large square area: 7squared is 49 inches. now you have 4 shaded triangles inside the square, they are all the same area if you know some property of the triangle. calculate individual triangle area: 3 x 4 2 = 6. multiply that by 4 you have 24 inch for the area of the shaded triangles. 24 49.

Square Inscribed In A Triangle Geometry Video Youtube Half of an equilateral triangle (aep) is 30 60 90 triangle, and sides are in the ratio of a:a√3:2a. a=x 2 (half of the side of the equilateral triangle) ap=√3x 2. since it is inscribed circle, centriod and the center of the circle will be same. ap will be median, and centroid will divide it in 2:1 (2y:1y) 3y=ap=√3x 2. First calculate the large square area: 7squared is 49 inches. now you have 4 shaded triangles inside the square, they are all the same area if you know some property of the triangle. calculate individual triangle area: 3 x 4 2 = 6. multiply that by 4 you have 24 inch for the area of the shaded triangles. 24 49. Let side of square = s ac = b, bc = a, ab = c. fb = as b and ae = bs a as the colored triangles are similar to the bigger triangle. steps to calculate area (s^2) : 1)calculate gb and ad using right angle triangle rule for triangles gbf and ade. 2)calculate gd using right angle triangle rule for triangle gcd. 3) gd^2 = s^2. A square is inscribed in a circle or a polygon if its four vertices lie on the circumference of the circle or on the sides of the polygon. figure a shows a square inscribed in a circle. figure b shows a square inscribed in a triangle. figure c shows a square inscribed in a quadrilateral. 14 15 23 31 a square of perimeter.

Find Area Of Square Inscribed In Right Triangle B Geometry Amc8 Amc10 Let side of square = s ac = b, bc = a, ab = c. fb = as b and ae = bs a as the colored triangles are similar to the bigger triangle. steps to calculate area (s^2) : 1)calculate gb and ad using right angle triangle rule for triangles gbf and ade. 2)calculate gd using right angle triangle rule for triangle gcd. 3) gd^2 = s^2. A square is inscribed in a circle or a polygon if its four vertices lie on the circumference of the circle or on the sides of the polygon. figure a shows a square inscribed in a circle. figure b shows a square inscribed in a triangle. figure c shows a square inscribed in a quadrilateral. 14 15 23 31 a square of perimeter.

What Is The Area Of Triangle Area Of Square Right Triangle
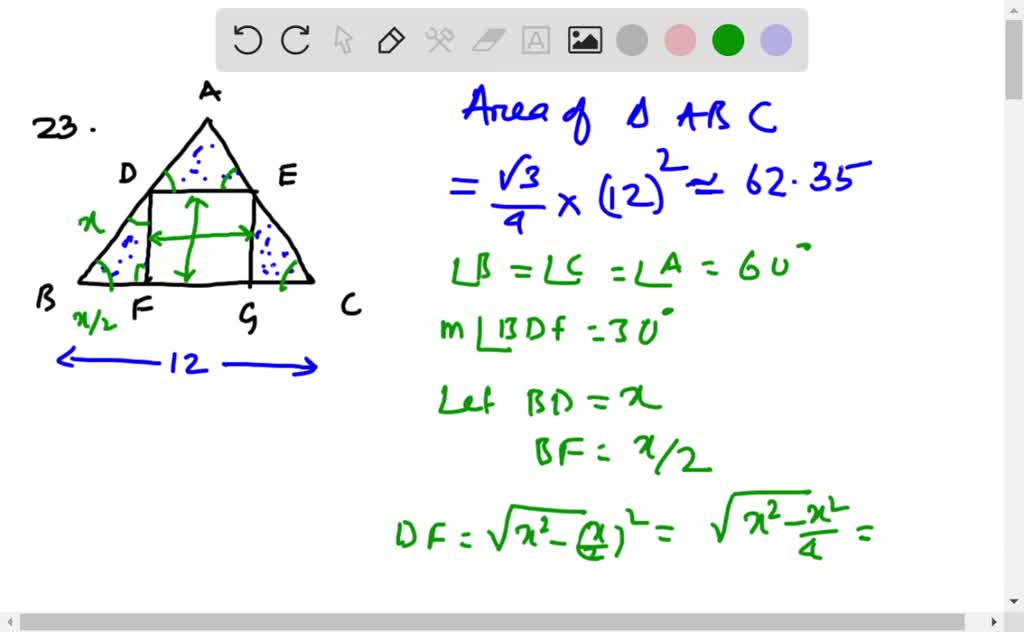
Solved A Square Is Inscribed In An Equilateral Triangle As Shown Find

Comments are closed.