Beam Fixed End Moments Formulas

Beam Fixed End Moments Formulas Beams fixed at one end and supported at the other continuous and point loads ; beams fixed at both ends continuous and point loads ; beam fixed at both ends single point load bending moment. m a = f a b 2 l 2 (1a) where . m a = moment at the fixed end a (nm, lb f ft) f = load (n, lb f) m b = f a 2 b l 2 (1b) where. %pdf 1.4 %âãÏÓ 9 0 obj > endobj xref 9 41 0000000016 00000 n 0000001363 00000 n 0000001440 00000 n 0000001568 00000 n 0000002035 00000 n 0000002389 00000 n 0000002423 00000 n 0000002499 00000 n 0000003452 00000 n 0000003610 00000 n 0000003852 00000 n 0000019053 00000 n 0000025583 00000 n 0000040804 00000 n 0000048046 00000 n 0000063687 00000 n 0000070381 00000 n 0000087573 00000 n.
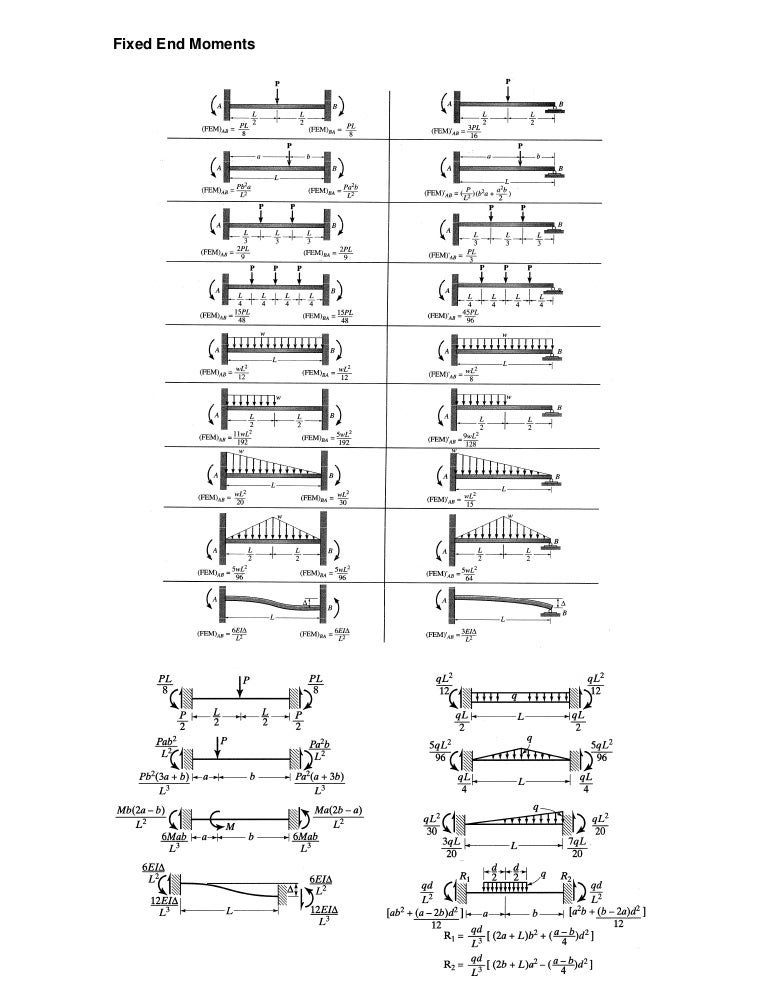
Table Of Fixed End Moments Formulas American forest & paper association american wood council 1111 19th street, nw suite 800 washington, dc 20036. phone: 202 463 4713 fax: 202 463 2791 [email protected] awc.org. Fixed at one end, supported concentrated load at any at point of load at fixed end 41) moment m max. m mal. beam fixed at shear moment both ends—concentrated load at any max. max. max. max. point when a < when a > when a < when a > b b b b pb2 pa 2 (a 3b) pab2 pa2b pab2 2pa3b2 3el (3a b) a pa3b3 3e11s pb2xa (3a1 — 3ax — 13 bx) pab 212 —. Beam design formulas simply select the picture which most resembles the beam configuration and loading condition you are interested in for a detailed summary of all the structural properties. beam equations for resultant forces, shear forces, bending moments and deflection can be found for each beam case shown. Beam overhanging both supports – unequal overhangs – uniformly distributed load. beam fixed at both ends – uniformly distributed load. beam fixed at both ends – concentrated load at center. beam fixed at both ends – concentrated load at any point. continuous beam – two equal spans – uniform load on one span.

Fixed End Beam Reaction Beam design formulas simply select the picture which most resembles the beam configuration and loading condition you are interested in for a detailed summary of all the structural properties. beam equations for resultant forces, shear forces, bending moments and deflection can be found for each beam case shown. Beam overhanging both supports – unequal overhangs – uniformly distributed load. beam fixed at both ends – uniformly distributed load. beam fixed at both ends – concentrated load at center. beam fixed at both ends – concentrated load at any point. continuous beam – two equal spans – uniform load on one span. The basic formulas for fixed end moments under these loads are: point load at the center of a beam: fem = p×l 8, where p is the point load and l is the length of the beam. uniformly distributed load: fem = w×l2 12, where w is the load per unit length and l is the beam length. these formulas provide a starting point for fem calculations, but. Summary for the value of end moments and deflection of perfectly restrained beam carrying various loadings. note that for values of eiy, y is positive downward. case 1: concentrated load anywhere on the span of fully restrained beam. mb = − pa2b l2. note: only for b > a. case 2: concentrated load on the midspan of fully restrained beam.

Fixed Ended Beam Bending Moments Youtube The basic formulas for fixed end moments under these loads are: point load at the center of a beam: fem = p×l 8, where p is the point load and l is the length of the beam. uniformly distributed load: fem = w×l2 12, where w is the load per unit length and l is the beam length. these formulas provide a starting point for fem calculations, but. Summary for the value of end moments and deflection of perfectly restrained beam carrying various loadings. note that for values of eiy, y is positive downward. case 1: concentrated load anywhere on the span of fully restrained beam. mb = − pa2b l2. note: only for b > a. case 2: concentrated load on the midspan of fully restrained beam.

Comments are closed.