Calculus 2 Ch 16 Hyperbolic Functions

Calculus 2 Ch 16 Hyperbolic Functions Youtube Share your videos with friends, family, and the world. Calculus of inverse hyperbolic functions. looking at the graphs of the hyperbolic functions, we see that with appropriate range restrictions, they all have inverses. most of the necessary range restrictions can be discerned by close examination of the graphs.

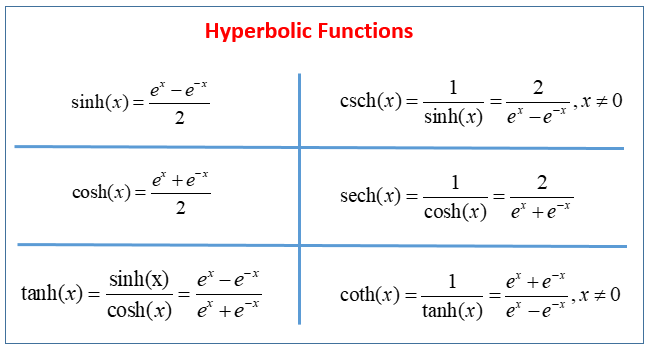
Hyperbolic Functions Examples Solutions Videos The other hyperbolic functions are then defined in terms of \(\sinh x\) and \(\cosh x\). the graphs of the hyperbolic functions are shown in figure \(\pageindex{1}\). figure \(\pageindex{1}\): graphs of the hyperbolic functions. it is easy to develop differentiation formulas for the hyperbolic functions. for example, looking at \(\sinh x\) we have. Hyperbolic functions are defined in terms of exponential functions. term by term differentiation yields differentiation formulas for the hyperbolic functions. these differentiation formulas give rise, in turn, to integration formulas. with appropriate range restrictions, the hyperbolic functions all have inverses. Hyperbolic functions are defined in terms of exponential functions. term by term differentiation yields differentiation formulas for the hyperbolic functions. these differentiation formulas give rise, in turn, to integration formulas. with appropriate range restrictions, the hyperbolic functions all have inverses. Show solution. 4. use the quotient rule to verify that tanh(x)′= sech2(x). tanh (x) ′ = sech 2 (x). 5. derive cosh2(x) sinh2(x)= cosh(2x) cosh 2 (x) sinh 2 (x) = cosh (2 x) from the definition. show solution. 6. take the derivative of the previous expression to find an expression for sinh(2x). sinh (2 x). 7.

Calculus Hyperbolic Functions Youtube Hyperbolic functions are defined in terms of exponential functions. term by term differentiation yields differentiation formulas for the hyperbolic functions. these differentiation formulas give rise, in turn, to integration formulas. with appropriate range restrictions, the hyperbolic functions all have inverses. Show solution. 4. use the quotient rule to verify that tanh(x)′= sech2(x). tanh (x) ′ = sech 2 (x). 5. derive cosh2(x) sinh2(x)= cosh(2x) cosh 2 (x) sinh 2 (x) = cosh (2 x) from the definition. show solution. 6. take the derivative of the previous expression to find an expression for sinh(2x). sinh (2 x). 7. Example 7.5.1: hyperangleacosh. add text here. solution. show that for the hyperbolic angle a of a point p = (x, y) on the unit hyperbola x2 − y2 = 1, the area a 2 of the hyperbolic sector \hypsector oap (the shaded region in the figure on the right) is. a 2 = 1 2 cosh − 1x . What you’ll learn to do: use integrals and derivatives to evaluate hyperbolic functions. we were introduced to hyperbolic functions in module 1: functions and graphs, along with some of their basic properties. in this section, we look at differentiation and integration formulas for the hyperbolic functions and their inverses.

Calculus Hyperbolic Functions Video Lessons Examples And Solutions 5a4 Example 7.5.1: hyperangleacosh. add text here. solution. show that for the hyperbolic angle a of a point p = (x, y) on the unit hyperbola x2 − y2 = 1, the area a 2 of the hyperbolic sector \hypsector oap (the shaded region in the figure on the right) is. a 2 = 1 2 cosh − 1x . What you’ll learn to do: use integrals and derivatives to evaluate hyperbolic functions. we were introduced to hyperbolic functions in module 1: functions and graphs, along with some of their basic properties. in this section, we look at differentiation and integration formulas for the hyperbolic functions and their inverses.

Hyperbolic Functions And Calculus By Joan Kessler Tpt

Introduction To Hyperbolic Functions Mr Mathematics