Calculus 2 Hyperbolic Functions 16 Of 57 Determine Cosh Xcoshx Etc

Calculus 2 Hyperbolic Functions 16 Of 57 Determine Cosh X Cosh X Visit ilectureonline for more math and science lectures!in this video i will determine cosh( x)=?, sinh( x)=?, tanh=?, coth( x)=?, sech( x)=?, and. Visit ilectureonline for more math and science lectures!in this video i will solve cosh(x y)=?next video in the series can be seen at: yout.

Calculus Hyperbolic Functions Video Lessons Examples And Solutions 5a4 4. use the quotient rule to verify that tanh(x)′= sech2(x). tanh (x) ′ = sech 2 (x). 5. derive cosh2(x) sinh2(x)= cosh(2x) cosh 2 (x) sinh 2 (x) = cosh (2 x) from the definition. show solution. 6. take the derivative of the previous expression to find an expression for sinh(2x). sinh (2 x). 7. Let’s take a moment to compare the derivatives of the hyperbolic functions with the derivatives of the standard trigonometric functions. there are a lot of similarities, but differences as well. for example, the derivatives of the sine functions match: \[\dfrac{d}{dx} \sin x=\cos x \nonumber \] and \[\dfrac{d}{dx} \sinh x=\cosh x. \nonumber \]. Learning objectives. 6.9.1 apply the formulas for derivatives and integrals of the hyperbolic functions.; 6.9.2 apply the formulas for the derivatives of the inverse hyperbolic functions and their associated integrals. And (d d x) sinh x = cosh x. the derivatives of the cosine functions, however, differ in sign: (d d x) cos x = − sin x, but (d d x) cosh x = sinh x. as we continue our examination of the hyperbolic functions, we must be mindful of their similarities and differences to the standard trigonometric functions.

Calculus 2 Hyperbolic Functions 6 Of 57 Graphical Representation Of Learning objectives. 6.9.1 apply the formulas for derivatives and integrals of the hyperbolic functions.; 6.9.2 apply the formulas for the derivatives of the inverse hyperbolic functions and their associated integrals. And (d d x) sinh x = cosh x. the derivatives of the cosine functions, however, differ in sign: (d d x) cos x = − sin x, but (d d x) cosh x = sinh x. as we continue our examination of the hyperbolic functions, we must be mindful of their similarities and differences to the standard trigonometric functions. The hyperbolic functions appear with some frequency in applications, and are quite similar in many respects to the trigonometric functions. this is a bit surprising given our initial definitions. definition 4.11.1 the hyperbolic cosine is the function coshx = ex e − x 2, and the hyperbolic sine is the function sinhx = ex − e − x 2. . 2.1 definitions. the hyperbolic cosine function, written cosh x, is defined for all real values of x by the relation. 1. cosh x = ex x. e. 2 ( ) ion, sinh x, is defined by1sinh x =(ex e x2 )the names of these two hyperbolic functions suggest that they have similar properties to the trigonome. ctivity 1show t.
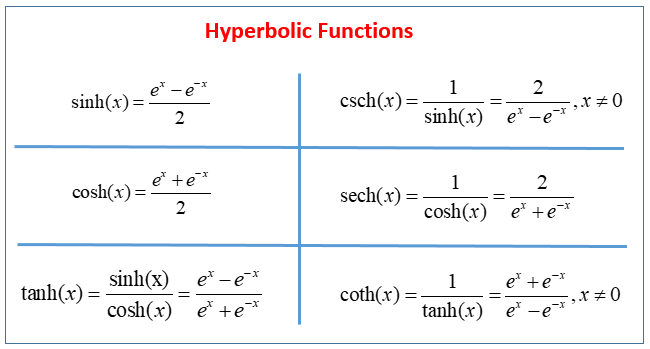
Hyperbolic Functions Examples Solutions Videos The hyperbolic functions appear with some frequency in applications, and are quite similar in many respects to the trigonometric functions. this is a bit surprising given our initial definitions. definition 4.11.1 the hyperbolic cosine is the function coshx = ex e − x 2, and the hyperbolic sine is the function sinhx = ex − e − x 2. . 2.1 definitions. the hyperbolic cosine function, written cosh x, is defined for all real values of x by the relation. 1. cosh x = ex x. e. 2 ( ) ion, sinh x, is defined by1sinh x =(ex e x2 )the names of these two hyperbolic functions suggest that they have similar properties to the trigonome. ctivity 1show t.

Calculus 2 Hyperbolic Functions 14 Of 57 Determine Cosh X Y Youtube

Comments are closed.