Calculus Hyperbolic Functions Why Are They Named With Trig Functions

Hyperbolic Trig Functions Explained W 15 Examples Tour start here for a quick overview of the site help center detailed answers to any questions you might have. Neat. the hyperbolic functions are like "half exponentials" because it takes two derivatives to complete the cycle. this is why they're useful in calculus not because we care about the coordinates on a hyperbola! understanding integral tables. you'll see hyperbolic functions in tables of tricky integrals and derivatives: ignore the specifics.

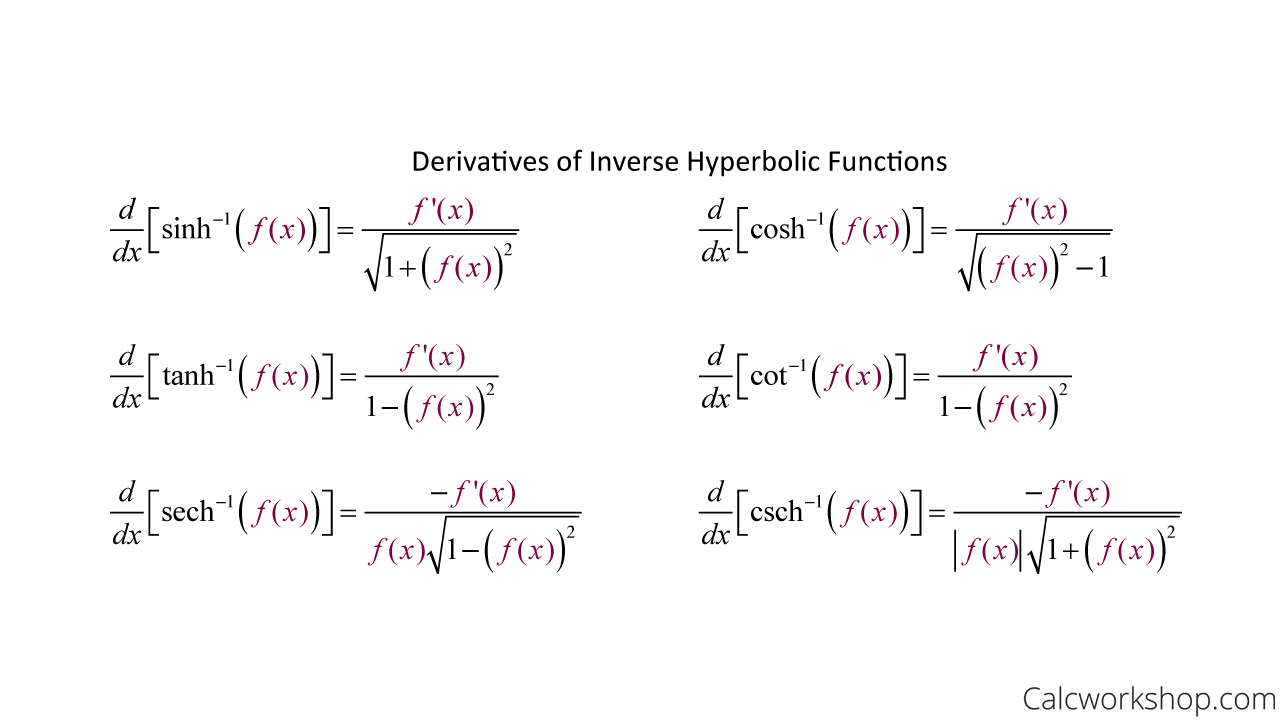
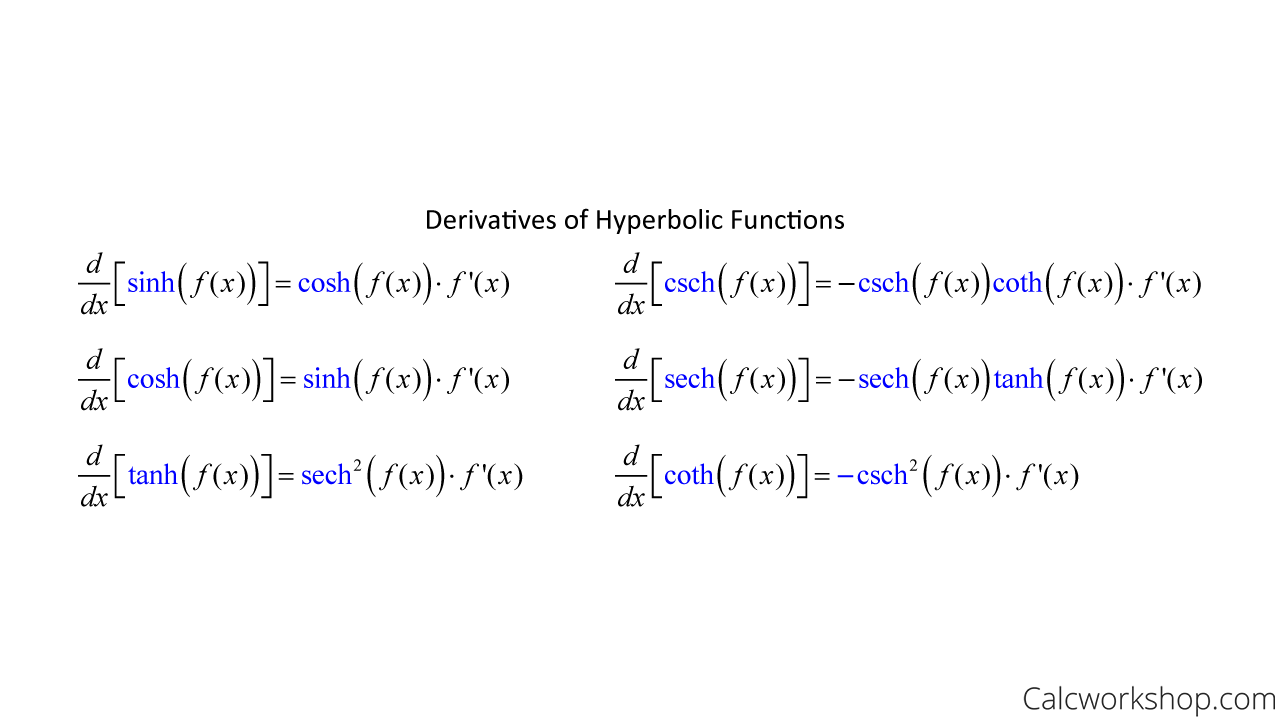
Hyperbolic Trig Functions Explained W 15 Examples Calculus of inverse hyperbolic functions. looking at the graphs of the hyperbolic functions, we see that with appropriate range restrictions, they all have inverses. most of the necessary range restrictions can be discerned by close examination of the graphs. Calculus of inverse hyperbolic functions. looking at the graphs of the hyperbolic functions, we see that with appropriate range restrictions, they all have inverses. most of the necessary range restrictions can be discerned by close examination of the graphs. And the derivatives of the hyperbolic trig functions are easily computed, and you will undoubtedly see the similarities to the well known trigonometric derivatives. notice, however, that some of the signs are different, as noted by whitman college. in particular, sinh, cosh, and tanh, or as i like to refer to them as the “ big three,” are. The inverse of a hyperbolic function is called an inverse hyperbolic function. for example, if x = sinh y, then y = sinh 1 x is the inverse of the hyperbolic sine function. the inverse hyperbolic functions expressed in terms of logarithmic functions are shown below: sinh 1 x = ln (x √(x 2 1)) cosh 1 x = ln (x √(x 2 1)).

Calculus Hyperbolic Functions Why Are They Named With Trig Functions And the derivatives of the hyperbolic trig functions are easily computed, and you will undoubtedly see the similarities to the well known trigonometric derivatives. notice, however, that some of the signs are different, as noted by whitman college. in particular, sinh, cosh, and tanh, or as i like to refer to them as the “ big three,” are. The inverse of a hyperbolic function is called an inverse hyperbolic function. for example, if x = sinh y, then y = sinh 1 x is the inverse of the hyperbolic sine function. the inverse hyperbolic functions expressed in terms of logarithmic functions are shown below: sinh 1 x = ln (x √(x 2 1)) cosh 1 x = ln (x √(x 2 1)). In some textbooks you might see the sine and cosine functions called circular functions, since any point on the unit circle \(x^2 y^2=1\) can be defined in terms of those functions (see figure [fig:cirangle]). those definitions motivate a similar idea for the unit hyperbola \(x^2 y^2=1\), whose points can be defined in terms of hyperbolic. Hyperbolic functions occur in the calculations of angles and distances in hyperbolic geometry. they also occur in the solutions of many linear differential equations (such as the equation defining a catenary), cubic equations, and laplace's equation in cartesian coordinates. laplace's equations are important in many areas of physics, including.

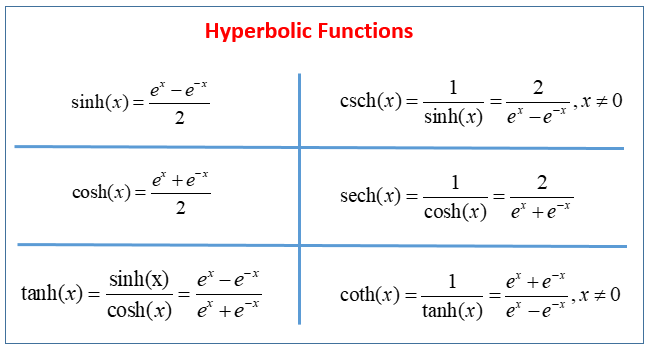
Hyperbolic Functions Examples Solutions Videos In some textbooks you might see the sine and cosine functions called circular functions, since any point on the unit circle \(x^2 y^2=1\) can be defined in terms of those functions (see figure [fig:cirangle]). those definitions motivate a similar idea for the unit hyperbola \(x^2 y^2=1\), whose points can be defined in terms of hyperbolic. Hyperbolic functions occur in the calculations of angles and distances in hyperbolic geometry. they also occur in the solutions of many linear differential equations (such as the equation defining a catenary), cubic equations, and laplace's equation in cartesian coordinates. laplace's equations are important in many areas of physics, including.

Calculus Hyperbolic Functions Why Are They Named With Trig Functions

Hyperbolic Trig Functions Explained W 15 Examples