Calculus Of Hyperbolic Functions
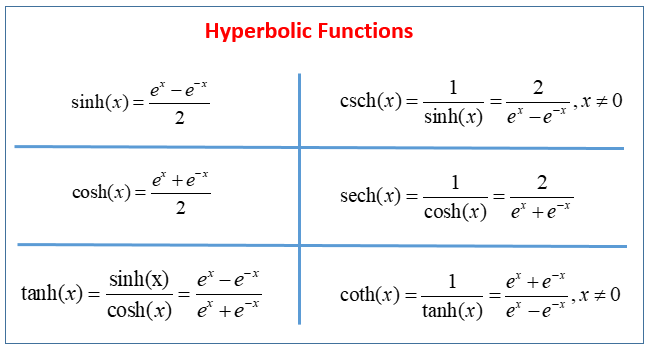
Hyperbolic Functions Examples Solutions Videos Hyperbolic functions are defined in terms of exponential functions. term by term differentiation yields differentiation formulas for the hyperbolic functions. these differentiation formulas give rise, in turn, to integration formulas. with appropriate range restrictions, the hyperbolic functions all have inverses. Calculus of inverse hyperbolic functions looking at the graphs of the hyperbolic functions, we see that with appropriate range restrictions, they all have inverses. most of the necessary range restrictions can be discerned by close examination of the graphs.

Calculus Hyperbolic Functions Video Lessons Examples And Solutions The last set of functions that we’re going to be looking in this chapter at are the hyperbolic functions. in many physical situations combinations of \({{\bf{e}}^x}\) and \({{\bf{e}}^{ x}}\) arise fairly often. because of this these combinations are given names. there are six hyperbolic functions and they are defined as follows. Hyperbolic functions are defined in terms of exponential functions. term by term differentiation yields differentiation formulas for the hyperbolic functions. these differentiation formulas give rise, in turn, to integration formulas. with appropriate range restrictions, the hyperbolic functions all have inverses. Math 400: calculus i differential calculus (lecture notes) 1: critical concepts for calculus (lecture notes) 1.7: hyperbolic functions (lecture notes for augmented lectures) expand collapse global location. Derivatives and integrals of the hyperbolic functions. recall that the hyperbolic sine and hyperbolic cosine are defined as. sinhx = ex − e−x 2 and coshx = ex e−x 2. the other hyperbolic functions are then defined in terms of sinhx and coshx. the graphs of the hyperbolic functions are shown in the following figure. figure 1.

Calculus Hyperbolic Functions Youtube Math 400: calculus i differential calculus (lecture notes) 1: critical concepts for calculus (lecture notes) 1.7: hyperbolic functions (lecture notes for augmented lectures) expand collapse global location. Derivatives and integrals of the hyperbolic functions. recall that the hyperbolic sine and hyperbolic cosine are defined as. sinhx = ex − e−x 2 and coshx = ex e−x 2. the other hyperbolic functions are then defined in terms of sinhx and coshx. the graphs of the hyperbolic functions are shown in the following figure. figure 1. A quick investigation demonstrates the possibility that as x → ∞, and tanh(x) → − 1 as x → − ∞. the graphs of the other three hyperbolic functions can be sketched using the graphs of cosh(x), sinh(x), and tanh(x) (figure 1.7.6). 3. figure 1.7.6: the hyperbolic functions involve combinations of ex and e − x. What you’ll learn to do: use integrals and derivatives to evaluate hyperbolic functions. we were introduced to hyperbolic functions in module 1: functions and graphs, along with some of their basic properties. in this section, we look at differentiation and integration formulas for the hyperbolic functions and their inverses.

Hyperbolic Functions Video Lecture Calculus Mathematics A quick investigation demonstrates the possibility that as x → ∞, and tanh(x) → − 1 as x → − ∞. the graphs of the other three hyperbolic functions can be sketched using the graphs of cosh(x), sinh(x), and tanh(x) (figure 1.7.6). 3. figure 1.7.6: the hyperbolic functions involve combinations of ex and e − x. What you’ll learn to do: use integrals and derivatives to evaluate hyperbolic functions. we were introduced to hyperbolic functions in module 1: functions and graphs, along with some of their basic properties. in this section, we look at differentiation and integration formulas for the hyperbolic functions and their inverses.

Calculus Hyperbolic Functions Video Lessons Examples And Solutions 5a4

Comments are closed.