Can A Function Be Continuous At Only One Point
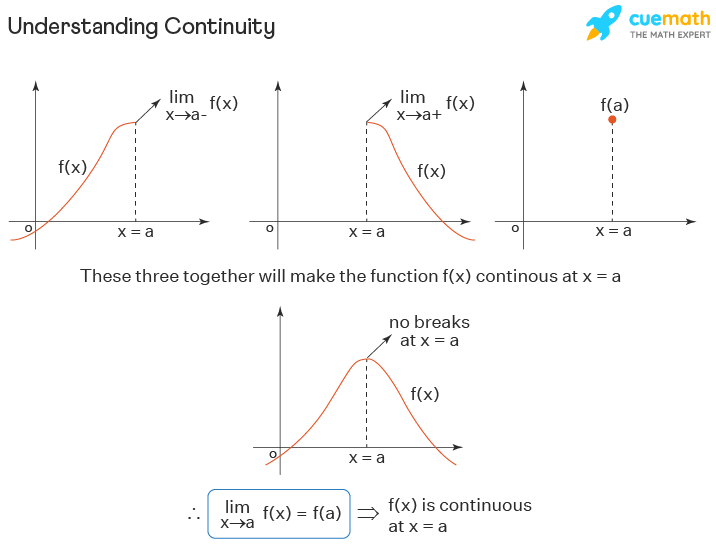
Continuous Function Definition Examples Continuity One standard example is the function. f(x) = {x, if x ∈ q 0, if x ∈ r ∖ q. that is, f(x) = x if x is rational, and f(x) = 0 if x is irrational. this function is continuous only at x = 0. added: the same basic idea can be used to build a function that is continuous at any single specified point. with a little more ingenuity, you can use it. 1) according to the definition given in spivak's book and also in , since $\lim {x\to1}f$ doesn't exist because $1$ is not an accumulation point, then the function is not continuous at $1$ (otherwise it should be $\lim {x\to 1}f=f(1)$). 2) according to this answer, as far as i can understand a function is continuous at an isolated point.

Continuity And One Sided Limits Ppt Download $\begingroup$ @maciejpiechotka: if you have a metric (or topological) space consisting only of one point, then the only converging (even the only existing) sequence is the constant sequence. hence, the continuity condition is trivially satisfied and every function having this space as domain is continuous. $\endgroup$ –. Continuity at a point; types of discontinuities; continuity over an interval; the intermediate value theorem; key concepts; glossary. contributors; summary: for a function to be continuous at a point, it must be defined at that point, its limit must exist at the point, and the value of the function at that point must equal the value of the limit at that point. Example: how about this piecewise function: it looks like this: it is defined at x=1, because h(1)=2 (no "hole") but at x=1 you can't say what the limit is, because there are two competing answers: "2" from the left, and "1" from the right; so in fact the limit does not exist at x=1 (there is a "jump") and so the function is not continuous. A function is continuous on an open interval if the interval is contained in the function's domain and the function is continuous at every interval point. a function that is continuous on the interval (, ) (the whole real line) is often called simply a continuous function; one also says that such a function is continuous everywhere.
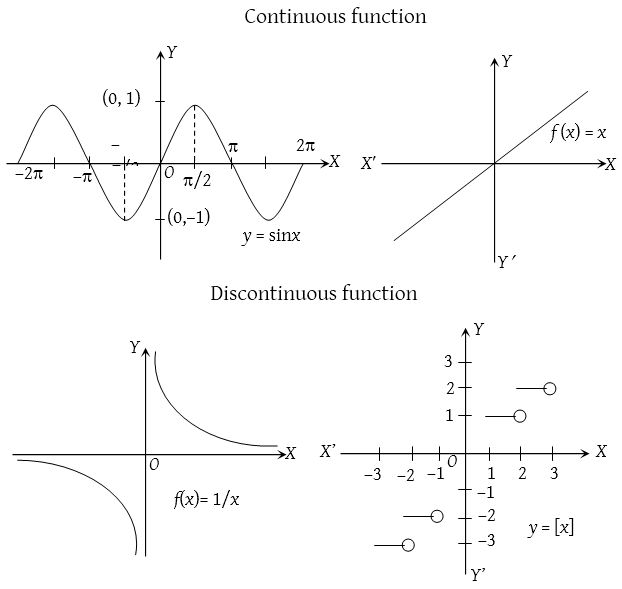
Continuous Function Cbse Library Example: how about this piecewise function: it looks like this: it is defined at x=1, because h(1)=2 (no "hole") but at x=1 you can't say what the limit is, because there are two competing answers: "2" from the left, and "1" from the right; so in fact the limit does not exist at x=1 (there is a "jump") and so the function is not continuous. A function is continuous on an open interval if the interval is contained in the function's domain and the function is continuous at every interval point. a function that is continuous on the interval (, ) (the whole real line) is often called simply a continuous function; one also says that such a function is continuous everywhere. Intuitively, a function is continuous at a particular point if there is no break in its graph at that point. continuity at a point. before we look at a formal definition of what it means for a function to be continuous at a point, let’s consider various functions that fail to meet our intuitive notion of what it means to be continuous at a point. Every other point f(x) is continuous, and since 0 is not in its domain this means f(x) is continuous everywhere in its domain and therefore continuous!1 in other words, a function can have a discontinuity and still be continuous. counterintu itive as the terminology is, it’s essentially our only choice, and it does address the problem.

Continuous And Uniformly Continuous Functions Youtube Intuitively, a function is continuous at a particular point if there is no break in its graph at that point. continuity at a point. before we look at a formal definition of what it means for a function to be continuous at a point, let’s consider various functions that fail to meet our intuitive notion of what it means to be continuous at a point. Every other point f(x) is continuous, and since 0 is not in its domain this means f(x) is continuous everywhere in its domain and therefore continuous!1 in other words, a function can have a discontinuity and still be continuous. counterintu itive as the terminology is, it’s essentially our only choice, and it does address the problem.
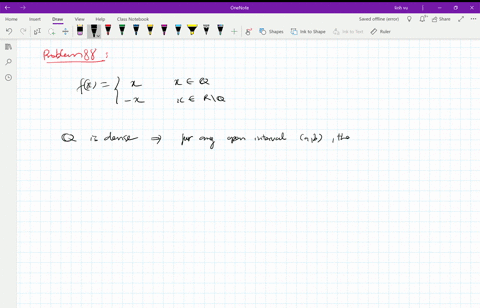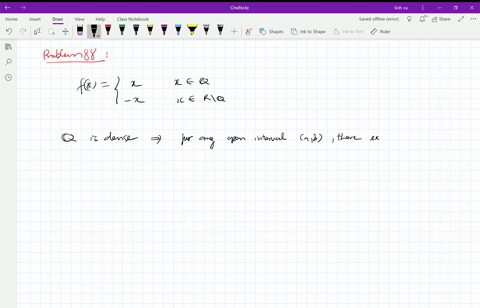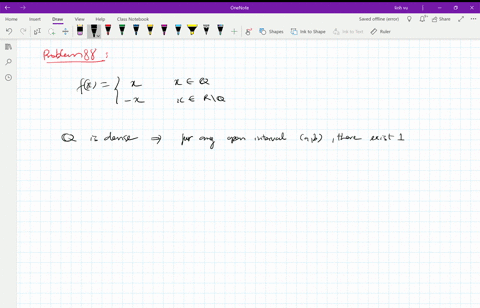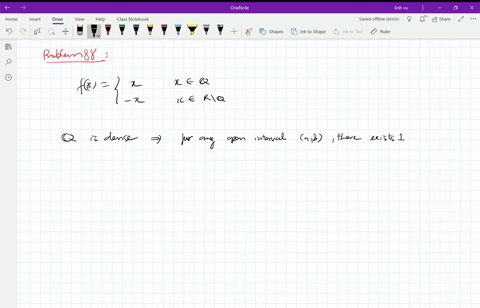
Solved Continuous At Only One Point Show That The Following Function Is

Constant Functions Are The Only Continuous Functions Discrete Metric

Comments are closed.