Cara Menentukan Sumbu Simetri Nilai Optimum Dan Titik Puncak Grafik Video pembelajaran ini membahas tentang cara menentukan sumbu simetri, nilai optimum dan koordinat titik puncak titik balik pada fungsi kuadrat. didalamnya t. Cara menentukan sumbu simetri nilai optimum dan titik puncak grafik fungsi kuadrat matematika kelas 9 smp bab 2.#grafikfungsikuadrat #nilaioptimum #titikoptumum.
Mencari Sumbu Simetri Dan Nilai Optimum Utakatikotak Pertama tama, kita perlu mengetahui bentuk fungsi kuadrat yang akan kita cari sumbu simetrinya. contoh: y = 2x^2 4x 5. 2. kemudian, kita perlu mencari nilai koefisien b pada bentuk umum fungsi kuadrat. dalam contoh di atas, nilai b adalah 4. 3. setelah mengetahui nilai b, kita dapat menggunakan rumus sumbu simetri berikut: x = b (2a) di. Dalam ilmu matematika, sumbu simetri dan nilai optimum adalah dua hal yang biasanya digunakan dalam penyelesaian persamaan dan fungsi kuadrat. advertisement sumbu simetri sendiri merupakan garis bayangan yang membagi dua bangun datar secara sama besar, sedangkan nilai optimum merupakan nilai optimum dan minumum dari suatu persamaan. Sumbu simetri adalah garis khayal yang membagi grafik fungsi kuadrat menjadi dua bagian yang simetris. sumbu simetri juga menentukan lokasi titik puncak atau lembah pada grafik fungsi kuadrat. selanjutnya, nilai optimum merujuk pada nilai minimum atau maksimum dari fungsi kuadrat. nilai optimum ini terjadi pada titik puncak atau lembah parabola. Baca juga: titik puncak grafik fungsi kuadrat: pengertian dan rumusnya. sumbu simetri grafik fungsi kuadrat disimbolkan dengan xp dan memiliki rumus sebagai berikut: dengan, xp: sumbu simetri atau posisi titik puncak di sumbu x. b: koefisien dari x pada fungsi kuadrat. a: koefisien dari x² pada fungsi kuadrat.
Fungsi Kuadrat вђјпёџ Titik Potong Sumbu X Sumbu Y Sumbu Simetri Nilai Sumbu simetri adalah garis khayal yang membagi grafik fungsi kuadrat menjadi dua bagian yang simetris. sumbu simetri juga menentukan lokasi titik puncak atau lembah pada grafik fungsi kuadrat. selanjutnya, nilai optimum merujuk pada nilai minimum atau maksimum dari fungsi kuadrat. nilai optimum ini terjadi pada titik puncak atau lembah parabola. Baca juga: titik puncak grafik fungsi kuadrat: pengertian dan rumusnya. sumbu simetri grafik fungsi kuadrat disimbolkan dengan xp dan memiliki rumus sebagai berikut: dengan, xp: sumbu simetri atau posisi titik puncak di sumbu x. b: koefisien dari x pada fungsi kuadrat. a: koefisien dari x² pada fungsi kuadrat. Assalamualaikum warahmatullahi wabarokatuh video pembelajaran ini membahas tentang cara menentukan titik potong sumbu x dan y, sumbu simetri, nilai optimum. A. karena a < 0, ini berarti grafik fungsi kuadrat nya berbentuk parabola yang terbuka ke bawah (menghadap ke bawah) b. sumbu simetri: c. nilai optimum: (nilai optimum ini merupakan nilai maksimum karena grafik fungsi kuadrat menghadap ke bawah) d. titik optimum : (1, 7) soal 2 . cari sumbu simetri dari grafik y = x² − 6x 5. penyelesaian:.
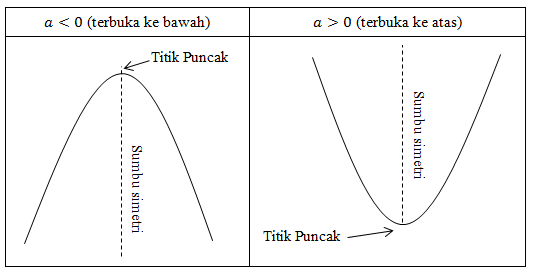
Mencari Sumbu Simetri Dan Nilai Optimum Utakatikotak Assalamualaikum warahmatullahi wabarokatuh video pembelajaran ini membahas tentang cara menentukan titik potong sumbu x dan y, sumbu simetri, nilai optimum. A. karena a < 0, ini berarti grafik fungsi kuadrat nya berbentuk parabola yang terbuka ke bawah (menghadap ke bawah) b. sumbu simetri: c. nilai optimum: (nilai optimum ini merupakan nilai maksimum karena grafik fungsi kuadrat menghadap ke bawah) d. titik optimum : (1, 7) soal 2 . cari sumbu simetri dari grafik y = x² − 6x 5. penyelesaian:.
Imath Cara Menentukan Sumbu Simetri Dan Titik Puncak Fungsi Kuadrat
Comments are closed.