Circle Circumscribing A Triangle Circle Inscribed In A Triangle Area Equilateral Triangle

Circle Circumscribing A Triangle Circle Inscribed In A Triangle In the first two cases, draw a perpendicular line segment from o to ¯ ab at the point d. figure 2.5.2 circumscribed circle for abc. the radii ¯ oa and ¯ ob have the same length r, so aob is an isosceles triangle. thus, from elementary geometry we know that ¯ od bisects both the angle ∠aob and the side ¯ ab. 5. yes. if you're familiar with construction using compass and straight edge, one of the easiest ways to construct an equilateral triangle is to draw two circles where each circle's centre lies on the other circle's edge. drawing a line between the two intersection points and then from each intersection point to the point on one circle farthest.
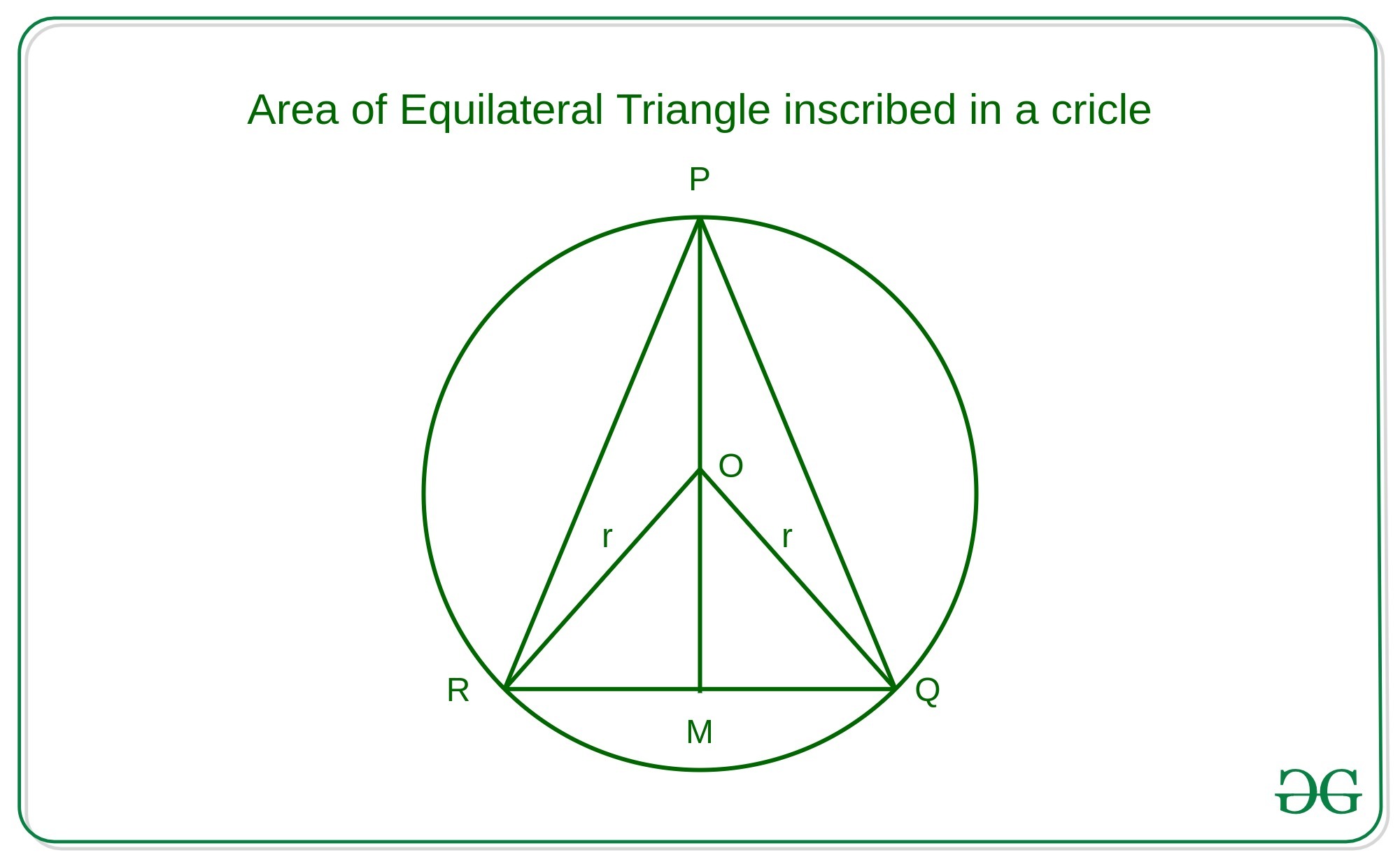
Area Of Equilateral Triangle Inscribed In A Circle Of Radius R For an obtuse triangle, the circumcenter is outside the triangle. when a circle inscribes a triangle, the triangle is outside of the circle and the circle touches the sides of the triangle at one point on each side. the sides of the triangle are tangent to the circle. to drawing an inscribed circle inside an isosceles triangle, use the angle. Konstantinos michailidis. nov 22, 2015. let abc equatorial triangle inscribed in the circle with radius r. applying law of sine to the triangle obc, we get. a sin60 = r sin30 ⇒ a = r ⋅ sin60 sin30 ⇒ a = √3 ⋅ r. now the area of the inscribed triangle is. a = 1 2 ⋅ am ⋅ bc. now am = ao om = r r ⋅ sin30 = 3 2 ⋅ r. and bc = a. We can use the properties of an equilateral triangle and a 30 60 90 right triangle to find the area of a circle inside an equilateral triangle, using only the triangle's side length. problem. an equilateral triangle has side length x. find the circle's area in terms of x. strategy. The radius of the circumscribed circle, known as the circumradius, can be calculated using the formula: r = (abc) (4Δ), where a, b, and c are the lengths of the triangle’s sides, and Δ represents the area of the triangle. maximum circle. the circumscribed circle has the largest possible radius among all circles drawn around the triangle.
Circumscribed Equilateral Triangle We can use the properties of an equilateral triangle and a 30 60 90 right triangle to find the area of a circle inside an equilateral triangle, using only the triangle's side length. problem. an equilateral triangle has side length x. find the circle's area in terms of x. strategy. The radius of the circumscribed circle, known as the circumradius, can be calculated using the formula: r = (abc) (4Δ), where a, b, and c are the lengths of the triangle’s sides, and Δ represents the area of the triangle. maximum circle. the circumscribed circle has the largest possible radius among all circles drawn around the triangle. Find area, given equilateral triangle and radius \alpha \beta prove inscribed parallelogram. circumscribe circle. R radius of inscribed circle o center of circumscribed circle i center of inscribed circle h a;h b;h c altitudes to sides a;b;c s = 1 2 h aa = 1 2 h bb = 1 2 h cc area of the triangle p = a b c 2 semi perimeter escribde cicler is a circle tangent to one of the sides and the extensions of the two other sides. a triangle has 3 escribed circles.

Formulas Radius Of Inscribed And Circumscribed Circle In A Triangle Find area, given equilateral triangle and radius \alpha \beta prove inscribed parallelogram. circumscribe circle. R radius of inscribed circle o center of circumscribed circle i center of inscribed circle h a;h b;h c altitudes to sides a;b;c s = 1 2 h aa = 1 2 h bb = 1 2 h cc area of the triangle p = a b c 2 semi perimeter escribde cicler is a circle tangent to one of the sides and the extensions of the two other sides. a triangle has 3 escribed circles.

How To Inscribe An Equilateral Triangle In A Circle Geometry Study

Comments are closed.