Circle With Two Tangents Drawn From An External Point Clipart Et
Circle With Two Tangents Drawn From An External Point Clipart Etc Illustration of a circle which illustrates that the tangents to a circle drawn from an external point are equal, and make equal angles with the line joining the point to the center. this app works best with javascript enabled. So, to convert the unit circle tangent lines into the original coordinate system, apply the three transformations in reverse order, i.e., if m = rst is the transformation that maps points into the unit circle’s coordinate system, then the tangents are lm = [1: ∓ √d2 − 1: d]rst. for the circle (x − h)2 (y − k)2 = r2 and point p.
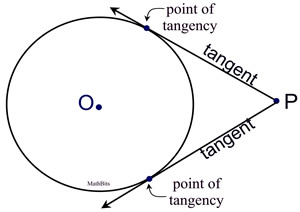
Construct Tangents To Circles Mathbitsnotebook Geo Remove parentheses and subtract 360 from both sides: –2∠mjp –2∠ojm = –180. divide through by –2:: ∠mjp ∠ojm = 90. 8. jp is a tangent to circle o and passes through p. jp is a tangent to o because it touches the circle at j and is at right angles to a radius at the contact point. (see tangent to a circle.). Transcript. theorem 10.2 (method 1) the lengths of tangents drawn from an external point to a circle are equal. given: let circle be with centre o and p be a point outside circle pq and pr are two tangents to circle intersecting at point q and r respectively to prove: lengths of tangents are equal i.e. pq = pr construction: join oq , or and op proof: as pq is a tangent oq ⊥ pq so, ∠ oqp. 2. the two tangents are equally inclined to the line joining the point to the centre of the circle. ∠mto = ∠nto, as ∆tom ≅ ∆ton. alternate segments. in the given below figure, the chord mn divides the circle into two segments. the tangent xy is drawn that touches the circle n. the alternate segment for ∠mny is the segment man and. Transcript. ex 10.2,10 prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre. given: a circle with center o. tangents pa and pb drawn from external point p to prove: apb aob = 180 proof: in quadrilateral.

From An External Point P Two Tangents Pa And Pb Are Drawn To A Circle 2. the two tangents are equally inclined to the line joining the point to the centre of the circle. ∠mto = ∠nto, as ∆tom ≅ ∆ton. alternate segments. in the given below figure, the chord mn divides the circle into two segments. the tangent xy is drawn that touches the circle n. the alternate segment for ∠mny is the segment man and. Transcript. ex 10.2,10 prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre. given: a circle with center o. tangents pa and pb drawn from external point p to prove: apb aob = 180 proof: in quadrilateral. Two tangents are drawn to a circle from an external point p. touching the circle at the points a and b. a third tangent intersects segment pa in c and segment pb in d and touches the circle at q. if pa = 20 units, find the perimeter of Δ pcd. Solution. let ap and bp be the two tangents to the circle with centre o. to prove : ap = bp. proof : in Δ aop and Δ bop. oa = ob (radii of the same circle) ∠oap =∠obp = 90∘ (since tangent at any point of a circle is perpendicular to the radius through the point of contact) op = op (common) ∴ Δaop ≅Δbop (by r.h.s. congruence criterion).
35 If Angle Between Two Tangents Drawn From An External Point P To A Two tangents are drawn to a circle from an external point p. touching the circle at the points a and b. a third tangent intersects segment pa in c and segment pb in d and touches the circle at q. if pa = 20 units, find the perimeter of Δ pcd. Solution. let ap and bp be the two tangents to the circle with centre o. to prove : ap = bp. proof : in Δ aop and Δ bop. oa = ob (radii of the same circle) ∠oap =∠obp = 90∘ (since tangent at any point of a circle is perpendicular to the radius through the point of contact) op = op (common) ∴ Δaop ≅Δbop (by r.h.s. congruence criterion).

Prove That The Angle Between The Two Tangents Drawn From An External

From An External Point P Two Tangents Pt And Ps Are Drawn To A Circle

Comments are closed.