Class 9 Chapter 8 Quadrilaterals Midpoint Theorem And Intercept

Class 9 Chapter 8 Quadrilaterals Midpoint Theorem And Intercept The main topics covered in ncert solutions for class 9 maths chapter 8 are given below: 8.1 introduction to quadrilaterals 8.2 angle sum property of a quadrilateral 8.3 types of quadrilaterals 8.4 properties of a parallelogram 8.5 another condition for a quadrilateral to be a parallelogram 8.6 the mid point theorem 8.7 summary. Ex 8.1 class 9 maths question 1. the angles of quadrilateral are in the ratio 3 : 5 : 9 : 13. find all the angles of the quadrilateral. solution: let the angles of the quadrilateral be 3x, 5x, 9x and 13x. ∴ 3x 5x 9x 13x = 360°. [angle sum property of a quadrilateral] ⇒ 30x = 360°. ⇒ x = 360∘ 30 = 12°.

Class 9 Chapter 8 Quadrilaterals Midpoint Theorem And Intercept Glance on maths chapter 8 class 9 quadrilaterals. chapter 8 of class 9 maths deals with the properties of parallelograms, the midpoint theorem, and the criteria for a quadrilateral to be a parallelogram. a parallelogram is a special type of quadrilateral(has 4 sides) where opposite sides are parallel and equal. A special condition to prove parallelogram a quadrilateral is a parallelogram if a pair of opposite sides is equal and parallel (theorem 8.8) mid point theorem, and its converse with proof (theorem 8.9 and theorem 8.10) here, the chapter is divided into 2 parts concept wise, and serial order wise. Some of the most important formulas and concepts covered in these ncert solutions for class 9 maths chapter 8 based on the angle sum property, parallelograms, and mid point theorem are given below: the sum of the angles of a quadrilateral is 360 degrees. a quadrilateral with equal and parallel pairs of opposite sides is called a parallelogram. These ncert solutions will help an individual to increase concentration and you can solve questions of supplementary books easily. 1. the angles of quadrilateral are in the ratio 3 : 5 : 9 : 13. find all the angles of the quadrilateral. let x be the common ratio between the angles. 2.
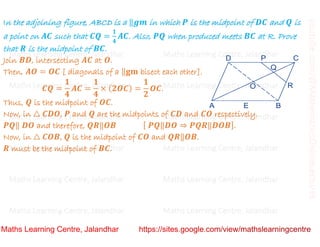
Class 9 Chapter 8 Quadrilaterals Midpoint Theorem And Intercept Theo Some of the most important formulas and concepts covered in these ncert solutions for class 9 maths chapter 8 based on the angle sum property, parallelograms, and mid point theorem are given below: the sum of the angles of a quadrilateral is 360 degrees. a quadrilateral with equal and parallel pairs of opposite sides is called a parallelogram. These ncert solutions will help an individual to increase concentration and you can solve questions of supplementary books easily. 1. the angles of quadrilateral are in the ratio 3 : 5 : 9 : 13. find all the angles of the quadrilateral. let x be the common ratio between the angles. 2. Mid point theorem : the line segment joining the mid points of any two sides of the triangle is parallel to the third side and is half of it. (i) in adc, s and r are the mid points of side ad and cd respectively. Solution: let the common ratio between the angles be = x. we know that the sum of the interior angles of the quadrilateral = 360° now, 3x 5x 9x 13x = 360° ⇒ 30x = 360° ⇒ x = 12°. , angles of the quadrilateral are: 3x = 3×12° = 36° 5x = 5×12° = 60° 9x = 9×12° = 108° 13x = 13×12° = 156°. 2. if the diagonals of a parallelogram.

Class 9 Chapter 8 Quadrilaterals Midpoint Theorem And Intercept Mid point theorem : the line segment joining the mid points of any two sides of the triangle is parallel to the third side and is half of it. (i) in adc, s and r are the mid points of side ad and cd respectively. Solution: let the common ratio between the angles be = x. we know that the sum of the interior angles of the quadrilateral = 360° now, 3x 5x 9x 13x = 360° ⇒ 30x = 360° ⇒ x = 12°. , angles of the quadrilateral are: 3x = 3×12° = 36° 5x = 5×12° = 60° 9x = 9×12° = 108° 13x = 13×12° = 156°. 2. if the diagonals of a parallelogram.

Class 9 Chapter 8 Quadrilaterals Midpoint Theorem And Intercept

Comments are closed.