Classical Mechanics Hamiltonian Formulation Solution Of The Problem Of Hamiltonianisdefinedasthelegendretransformofthelagrangian h= p 1 1 p 2 2 l; where the generalized velocities 1 and 2 are expressed in terms of generalized. 4. the hamiltonian formalism we’ll now move onto the next level in the formalism of classical mechanics, due initially to hamilton around 1830. while we won’t use hamilton’s approach to solve any further complicated problems, we will use it to reveal much more of the structure underlying classical dynamics.
Ppt Hamiltonian Systems Powerpoint Presentation Free Download Id If you want to support this channel then you can become a member or donate here buymeacoffee advancedphysicsthis is completely voluntary, th. This chapter is to be read in conjunction with introduction to classical mechanics, with problems and solutions °c 2007, by david morin, cambridge university press. the text in this version is the same as in version 1, but some new problems and exercises have been added. more information on the book can be found at:. In terms of the hamiltonian, the equations of motion of a system are given by hamilton's equations: r˙i = ∂h ∂pi p˙i = −∂h ∂ri r ˙ i = ∂ h ∂ p i p ˙ i = − ∂ h ∂ r i. the solution of hamilton's equations of motion will yield a trajectory in terms of positions and momenta as functions of time. Failing that, if one can only show that a complete solution to this hamilton–jacobi equation does or does not exist, that will also resolve the question of existence of solutions. the method employed here is not specific to the navier–stokes problem or even to classical mechanics, and can be applied to any traditionally non hamiltonian problem.
Classical Mechanics Lagrangian And Hamiltonian Probs Solution In terms of the hamiltonian, the equations of motion of a system are given by hamilton's equations: r˙i = ∂h ∂pi p˙i = −∂h ∂ri r ˙ i = ∂ h ∂ p i p ˙ i = − ∂ h ∂ r i. the solution of hamilton's equations of motion will yield a trajectory in terms of positions and momenta as functions of time. Failing that, if one can only show that a complete solution to this hamilton–jacobi equation does or does not exist, that will also resolve the question of existence of solutions. the method employed here is not specific to the navier–stokes problem or even to classical mechanics, and can be applied to any traditionally non hamiltonian problem. This page titled 15.3: canonical transformations in hamiltonian mechanics is shared under a cc by nc sa 4.0 license and was authored, remixed, and or curated by douglas cline via source content that was edited to the style and standards of the libretexts platform. hamiltonian mechanics is an especially elegant and powerful way to derive the. Thus the hamiltonian is. h = p2r 2m p2ϕ 2mr2sin2 α mgr cos α. (14.4.3) (14.4.3) h = p r 2 2 m p ϕ 2 2 m r 2 sin 2 α m g r cos α. now we can obtain the equations of motion by applying equation d in turn to r r and ϕ ϕ and then equation c in turn to r r and ϕ ϕ:.
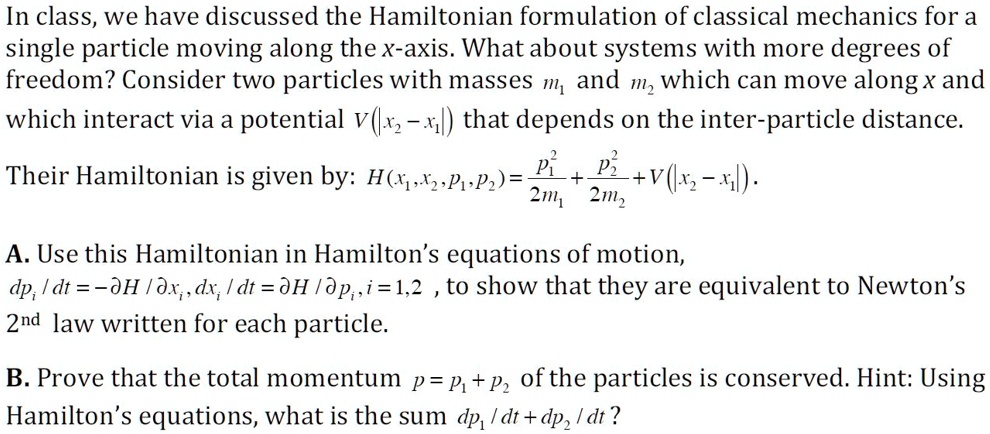
Solved In Class We Have Discussed The Hamiltonian Formulation Of This page titled 15.3: canonical transformations in hamiltonian mechanics is shared under a cc by nc sa 4.0 license and was authored, remixed, and or curated by douglas cline via source content that was edited to the style and standards of the libretexts platform. hamiltonian mechanics is an especially elegant and powerful way to derive the. Thus the hamiltonian is. h = p2r 2m p2ϕ 2mr2sin2 α mgr cos α. (14.4.3) (14.4.3) h = p r 2 2 m p ϕ 2 2 m r 2 sin 2 α m g r cos α. now we can obtain the equations of motion by applying equation d in turn to r r and ϕ ϕ and then equation c in turn to r r and ϕ ϕ:.
Solved I The Hamiltonian In Classical Mechanics Cm Is Chegg
Comments are closed.