Derivatives Of Hyperbolic Functions

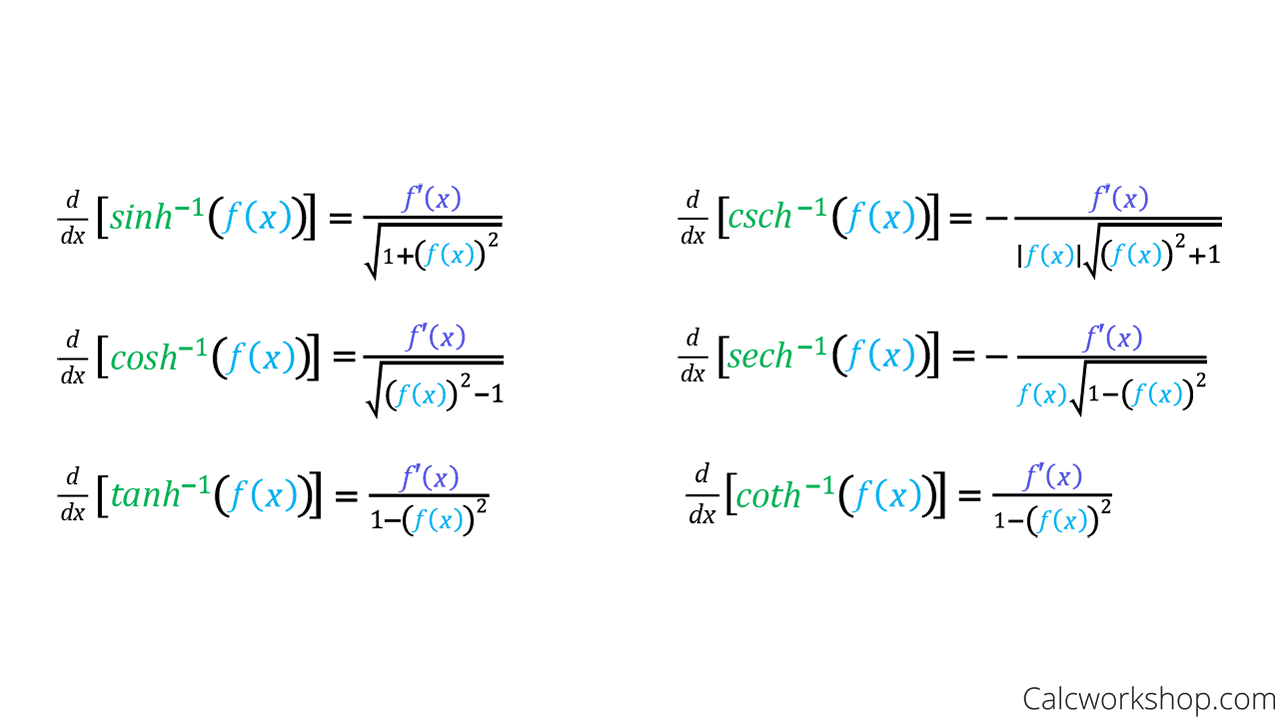
Derivatives Of Hyperbolic Functions 15 Powerful Examples Learn how to differentiate the six hyperbolic functions using exponential functions and quotient rule. see the graphs, identities and examples of hyperbolic functions and their derivatives. Learn how to calculate the derivative of hyperbolic functions using exponential functions and hyperbolic identities. see the formulas, proofs, graphs and applications of hyperbolic functions and their derivatives.

Lesson 13 Derivative Of Hyperbolic Functions Let’s take a moment to compare the derivatives of the hyperbolic functions with the derivatives of the standard trigonometric functions. there are a lot of similarities, but differences as well. for example, the derivatives of the sine functions match: \[\dfrac{d}{dx} \sin x=\cos x \nonumber \] and \[\dfrac{d}{dx} \sinh x=\cosh x. \nonumber \]. Learn how to differentiate hyperbolic functions and their inverses using exponential functions and inverse function theorem. see formulas, examples and a table of derivatives. Learn the formulas and properties of the hyperbolic functions and their inverses, and how to differentiate and integrate them. see examples, graphs, and applications of the hyperbolic functions and their derivatives. 3. derivatives. 3.1 the definition of the derivative; 3.2 interpretation of the derivative; 3.3 differentiation formulas; 3.4 product and quotient rule; 3.5 derivatives of trig functions; 3.6 derivatives of exponential and logarithm functions; 3.7 derivatives of inverse trig functions; 3.8 derivatives of hyperbolic functions; 3.9 chain rule.

Derivative Of Hyperbolic Functions Formula Proof Examples Learn the formulas and properties of the hyperbolic functions and their inverses, and how to differentiate and integrate them. see examples, graphs, and applications of the hyperbolic functions and their derivatives. 3. derivatives. 3.1 the definition of the derivative; 3.2 interpretation of the derivative; 3.3 differentiation formulas; 3.4 product and quotient rule; 3.5 derivatives of trig functions; 3.6 derivatives of exponential and logarithm functions; 3.7 derivatives of inverse trig functions; 3.8 derivatives of hyperbolic functions; 3.9 chain rule. The derivative of hyperbolic functions represents the rate of change of the hyperbolic functions involving the combination of e x and e x with respect to the variable. it is used to describe the shape of electrical wires or cables hanging freely between two poles, as well as to model satellite rings and planetary formations. hyperbolic sine (sinh). Learn how to differentiate and integrate the hyperbolic functions and their inverses, and how they relate to the standard trigonometric functions. see formulas, graphs, examples and applications of the hyperbolic functions.

Lesson 4 Derivative Of Inverse Hyperbolic Functions The derivative of hyperbolic functions represents the rate of change of the hyperbolic functions involving the combination of e x and e x with respect to the variable. it is used to describe the shape of electrical wires or cables hanging freely between two poles, as well as to model satellite rings and planetary formations. hyperbolic sine (sinh). Learn how to differentiate and integrate the hyperbolic functions and their inverses, and how they relate to the standard trigonometric functions. see formulas, graphs, examples and applications of the hyperbolic functions.

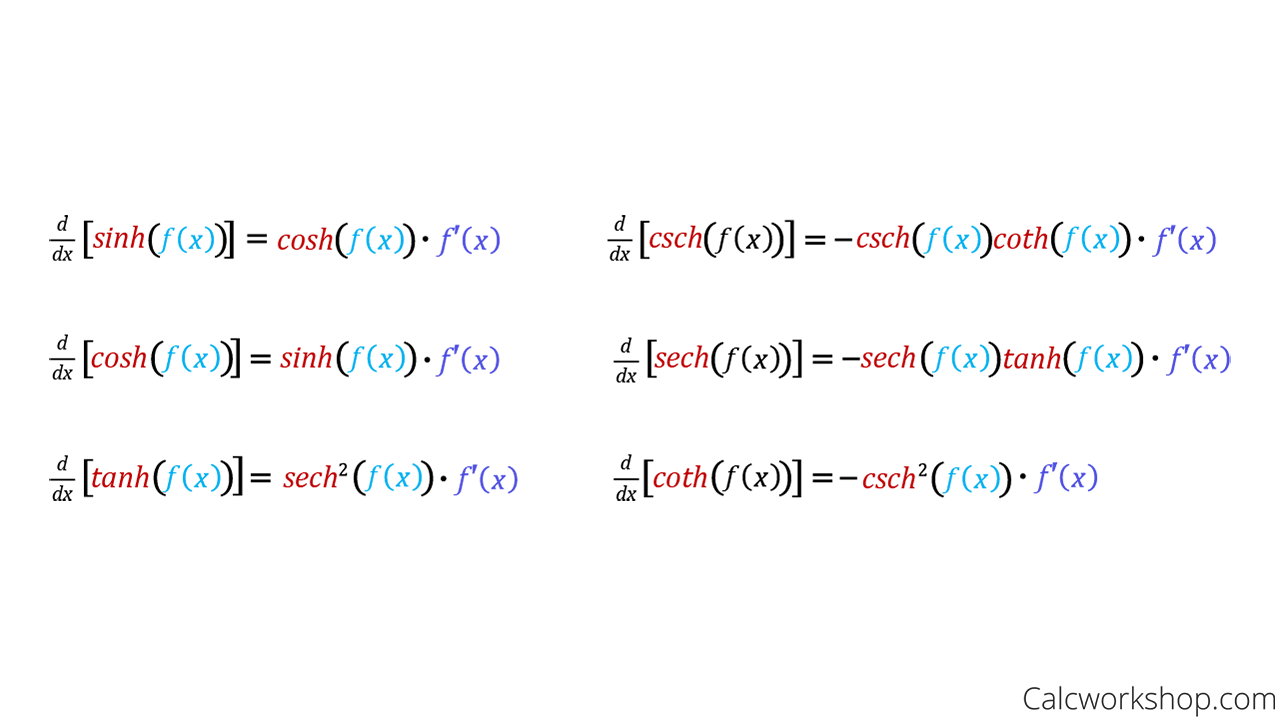
Hyperbolic Functions Examples

Lesson 13 Derivative Of Hyperbolic Functions