Descriptive Statistics Full Tutorial Mean Median Mode Variance Learn the basics of descriptive statistics in 15 minutes! if you're new to quantitative data analysis, you don't want to miss this. in this lesson, we cover. Descriptive statistics, although relatively simple, are a critically important part of any quantitative data analysis. measures of central tendency include the mean (average), median and mode. skewness indicates whether a dataset leans to one side or another; measures of dispersion include the range, variance and standard deviation.
Mean Median Mode And Standard Deviation Descriptive Statistics Youtube Types of descriptive statistics. there are 3 main types of descriptive statistics: the distribution concerns the frequency of each value. the central tendency concerns the averages of the values. the variability or dispersion concerns how spread out the values are. you can apply these to assess only one variable at a time, in univariate. 📈 measures of central tendency, including mean, median, and mode, describe the center or typical data point within a range of numbers. 📊 skewness is a statistic that measures the lean of data distribution to the left or right, impacting the interpretation of other statistics. Key aspects of descriptive statistics. measures of central tendency: descriptive statistics include calculating the mean, median, and mode, which offer insights into the center of the data distribution. measures of dispersion: variance, standard deviation, and range help us understand the spread or variability of the data. Measures of central tendency are summary statistics that represent the center point or typical value of a dataset. examples of these measures include the mean, median, and mode. these statistics indicate where most values in a distribution fall and are also referred to as the central location of a distribution.
Descriptive Statistics Mean Median And Mode Youtube Key aspects of descriptive statistics. measures of central tendency: descriptive statistics include calculating the mean, median, and mode, which offer insights into the center of the data distribution. measures of dispersion: variance, standard deviation, and range help us understand the spread or variability of the data. Measures of central tendency are summary statistics that represent the center point or typical value of a dataset. examples of these measures include the mean, median, and mode. these statistics indicate where most values in a distribution fall and are also referred to as the central location of a distribution. Descriptive statistics focus on summarising and describing the main features of a dataset. they provide simple summaries and visualisations, such as mean, median, mode, range, and standard deviation, to help understand the basic characteristics of the data. these statistics do not involve generalisations beyond the data at hand. Example 1: student grades. let’s say a teacher has the following set of grades for 7 students: 85, 90, 88, 92, 78, 88, and 94. the teacher could use descriptive statistics to summarize this data: median (middle value): first, rearrange the grades in ascending order (78, 85, 88, 88, 90, 92, 94). the median grade is 88.
How To Calculate Descriptive Statistics Of Panel Data Mean Median Descriptive statistics focus on summarising and describing the main features of a dataset. they provide simple summaries and visualisations, such as mean, median, mode, range, and standard deviation, to help understand the basic characteristics of the data. these statistics do not involve generalisations beyond the data at hand. Example 1: student grades. let’s say a teacher has the following set of grades for 7 students: 85, 90, 88, 92, 78, 88, and 94. the teacher could use descriptive statistics to summarize this data: median (middle value): first, rearrange the grades in ascending order (78, 85, 88, 88, 90, 92, 94). the median grade is 88.
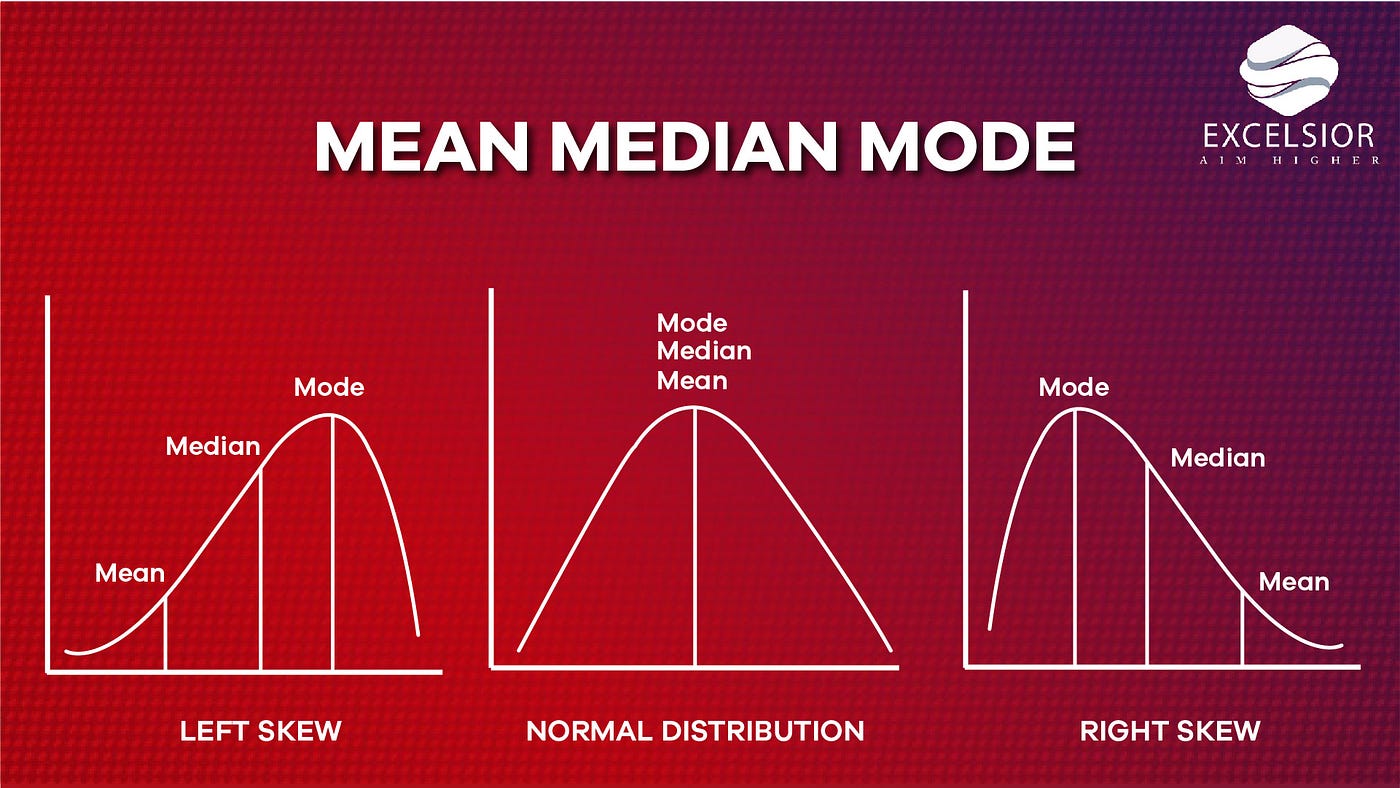
Mean Median Mode Introduction Explanation And Definition By
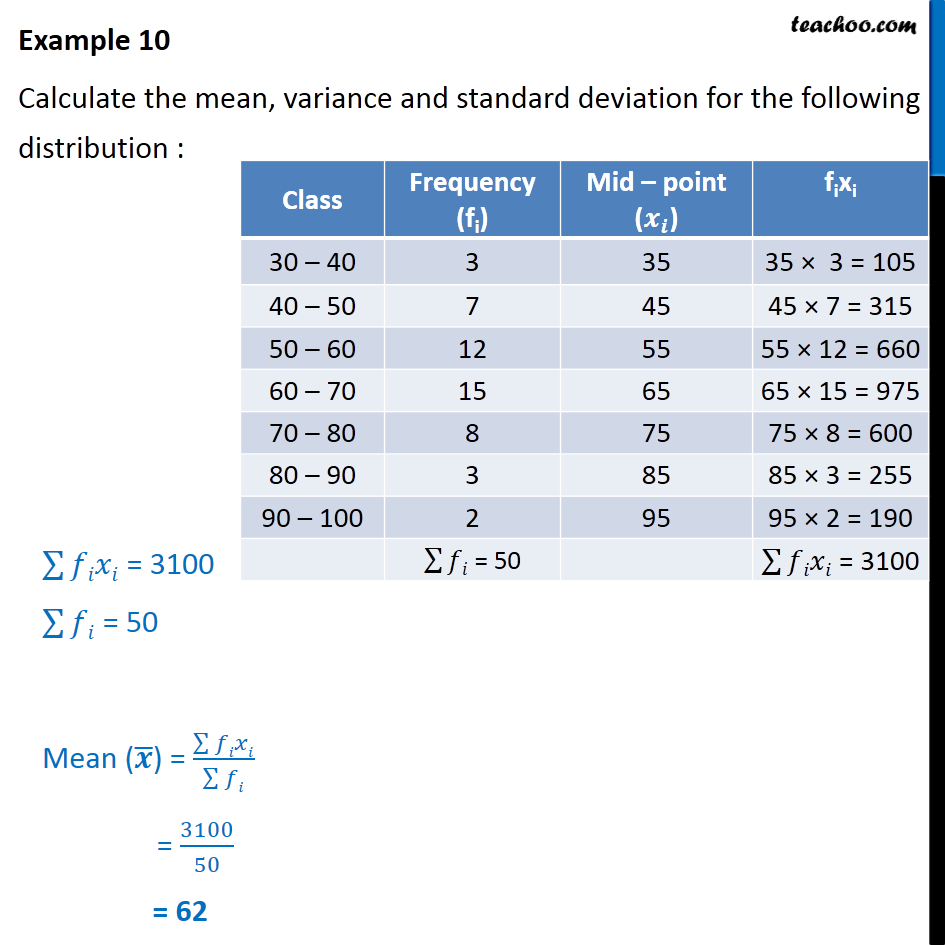
What Is The Use Of The Mean Standard Deviation And Variance In Your
Comments are closed.