Distributive Property Definition Solved Problems

Distributive Property Definition Solved Problems In this article, we learned about the distributive property, formulas, when to use the distributive property, and also how to use distributive property in complex equations and problems. let’s solve a few examples and practice problems based on the distributive property. solved examples on distributive property. example 1: solve $(5 7 3) 4$. The distributive property refers to the distributive property of multiplication and applies to both addition and subtraction. an expression in the form a × (b c) is solved as (a × b) (a × c) using the distributive property. here, a, b, and c are integers, and operand a is distributed among the other two operands, b and c.

Distributive Property Of Multiplication And Division Definition Example 1: distributive property with basic facts. show how to solve 3 \times 5 3 × 5 using the distributive property. identify an equation multiplying two numbers. you can use the distributive property with 3 \times 5, 3 × 5, since it is multiplication. 2 show one of the numbers being multiplied as a sum of numbers. Here's how to solve a multiple step solve for x algebra problem using the distributive property!full algebra 2 playlist: playlist?lis. The distributive property states that an expression which is given in form of a (b c) can be solved as a × (b c) = ab ac. this distributive law is also applicable to subtraction and is expressed as, a (b c) = ab ac. this means operand a is distributed between the other two operands. distributive property definition. Example 1: using the distributive property of multiplication over addition, solve the expression 10 (9 11). let us try to solve it by examining the expression 10 (9 11). we can start by multiplying 10 by addends that are 9 and 11 which are in the parenthesis. 10 × 9 10 × 11. = 90 110.
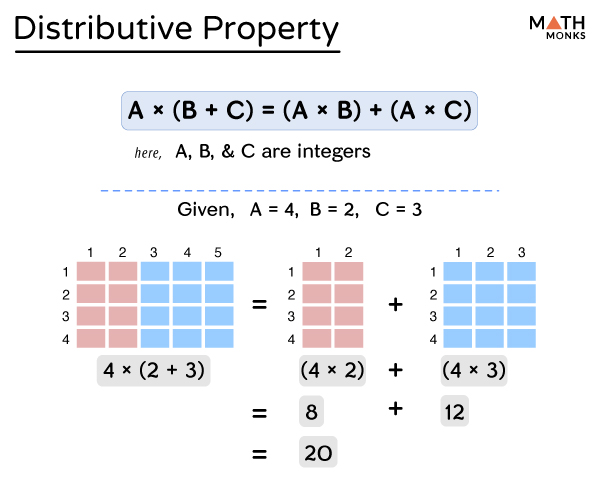
Distributive Property Law Definition Solved Examples Diagrams The distributive property states that an expression which is given in form of a (b c) can be solved as a × (b c) = ab ac. this distributive law is also applicable to subtraction and is expressed as, a (b c) = ab ac. this means operand a is distributed between the other two operands. distributive property definition. Example 1: using the distributive property of multiplication over addition, solve the expression 10 (9 11). let us try to solve it by examining the expression 10 (9 11). we can start by multiplying 10 by addends that are 9 and 11 which are in the parenthesis. 10 × 9 10 × 11. = 90 110. Apply the distributive property to the inner parentheses first, and combine like terms. finally, get rid of the square bracket symbol by distributing one more time. you can also use the distributive property when you solve equations. example 7: solve the linear equation below using the distributive property. In algebra, we use the distributive property to remove parentheses as we simplify expressions. for example, if we are asked to simplify the expression 3 (x 4), the order of operations says to work in the parentheses first. but we cannot add x and 4, since they are not like terms. so we use the distributive property, as shown in example 7.4.1.

Distributive Property Math Steps Examples Practice Questions Apply the distributive property to the inner parentheses first, and combine like terms. finally, get rid of the square bracket symbol by distributing one more time. you can also use the distributive property when you solve equations. example 7: solve the linear equation below using the distributive property. In algebra, we use the distributive property to remove parentheses as we simplify expressions. for example, if we are asked to simplify the expression 3 (x 4), the order of operations says to work in the parentheses first. but we cannot add x and 4, since they are not like terms. so we use the distributive property, as shown in example 7.4.1.

Distributive Property Law Definition Solved Examples Diagrams

Distributive Property Definition Mathmedia

Comments are closed.