Distributive Property Law вђ Definition Solved Examples Diagr
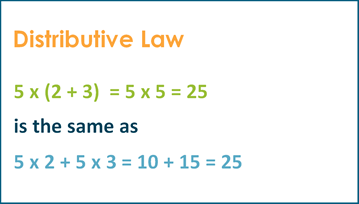
Distributive Law In Math K5 Learning Step 1: we first multiply the 2 addend by 9, which give us. 9 (20 – 5) = (9 × 20) – (9 × 5) = 180 – 45. step 2: subtracting the products together will give us the answer 135. let us solve another example using the distributive property of multiplication over subtraction. The distributive property states that an expression which is given in form of a (b c) can be solved as a × (b c) = ab ac. this distributive law is also applicable to subtraction and is expressed as, a (b c) = ab ac. this means operand a is distributed between the other two operands. distributive property definition.
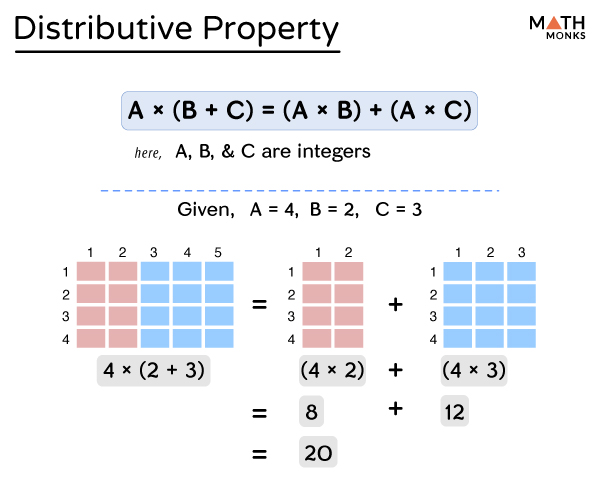
Distributive Property Law Definition Solved Examples Diagrams In this article, we learned about the distributive property, formulas, when to use the distributive property, and also how to use distributive property in complex equations and problems. let’s solve a few examples and practice problems based on the distributive property. solved examples on distributive property. example 1: solve $(5 7 3) 4$. Example 1: distributive property with basic facts. show how to solve 3 \times 5 3 × 5 using the distributive property. identify an equation multiplying two numbers. you can use the distributive property with 3 \times 5, 3 × 5, since it is multiplication. 2 show one of the numbers being multiplied as a sum of numbers. This property is particularly useful when dealing with algebraic expressions and equations involving division. the distributive property of division can be expressed as follows: \(a \div (b c) = a \div b a \div c\) let's explore a few distributive property formula examples to help us better understand the chi square formula. Multiplication and subtraction. the distributive property states that, for real numbers a, b, and c, two conditions are always true: a (b c) = ab ac. a (b c) = ab ac. you can use distributive property to turn one complex multiplication equation into two simpler multiplication problems, then add or subtract the two answers as required.

Distributive Property Definition Solved Problems This property is particularly useful when dealing with algebraic expressions and equations involving division. the distributive property of division can be expressed as follows: \(a \div (b c) = a \div b a \div c\) let's explore a few distributive property formula examples to help us better understand the chi square formula. Multiplication and subtraction. the distributive property states that, for real numbers a, b, and c, two conditions are always true: a (b c) = ab ac. a (b c) = ab ac. you can use distributive property to turn one complex multiplication equation into two simpler multiplication problems, then add or subtract the two answers as required. Applying the distributive property: examples. let's explore the distributive property further with some examples. example 1: solve the following expressions using the distributive property: (i) 4(2x 4 7x) (ii) 2x(x 2 y) (iii) 4(7xy 13yx) solution: using the distributive property, a ( b c) = ab ac, we can solve these expressions. Distributive property definition the distributive property is an algebraic property that is used to multiply a single value and two or more values within a set of parenthesis. the distributive property states that when a factor is multiplied by the sum addition of two terms, it is essential to multiply each of the two numbers by the factor, and.

Distributive Property Of Multiplication And Division Definition Applying the distributive property: examples. let's explore the distributive property further with some examples. example 1: solve the following expressions using the distributive property: (i) 4(2x 4 7x) (ii) 2x(x 2 y) (iii) 4(7xy 13yx) solution: using the distributive property, a ( b c) = ab ac, we can solve these expressions. Distributive property definition the distributive property is an algebraic property that is used to multiply a single value and two or more values within a set of parenthesis. the distributive property states that when a factor is multiplied by the sum addition of two terms, it is essential to multiply each of the two numbers by the factor, and.

Distributive Property

Comments are closed.