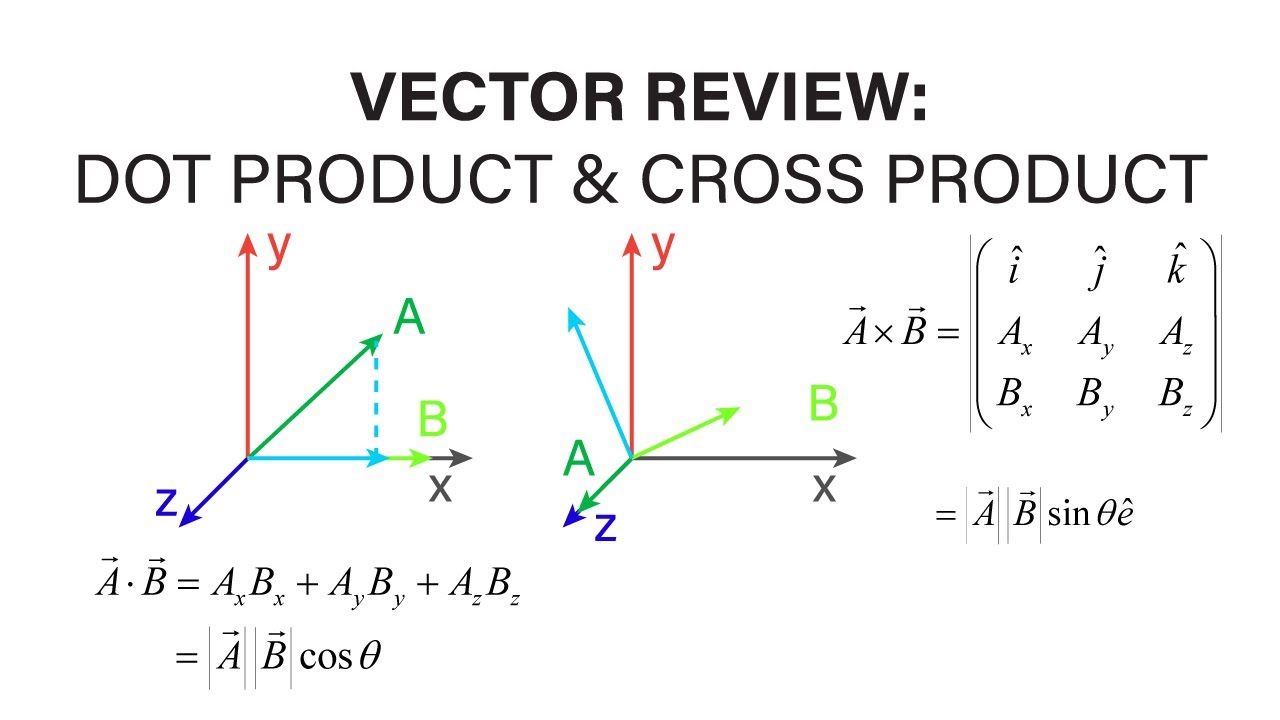
Introductory Fluid Mechanics Vector Review 2 Dot Product Cross 1.5: the dot and cross product. definition: the dot product. we define the dot product of two vectors v = aˆi bˆj and w = cˆi dˆj to be. v ⋅ w = ac bd. notice that the dot product of two vectors is a number and not a vector. for 3 dimensional vectors, we define the dot product similarly:. Here are two vectors: they can be multiplied using the "dot product" (also see cross product). calculating. the dot product is written using a central dot: a · b this means the dot product of a and b. we can calculate the dot product of two vectors this way: a · b = |a| × |b| × cos(θ) where: |a| is the magnitude (length) of vector a.
Dot Product Formula Examples Dot Product Of Two Vectors The dot product. there are two ways of multiplying vectors which are of great importance in applications. the first of these is called the dot product. when we take the dot product of vectors, the result is a scalar. for this reason, the dot product is also called the scalar product and sometimes the inner product. the definition is as follows. 1. adding →a to itself b times (b being a number) is another operation, called the scalar product. the dot product involves two vectors and yields a number. – user65203. may 22, 2014 at 22:40. something not mentioned but of interest is that the dot product is an example of a bilinear function, which can be considered a generalization of. In mathematics, the dot product or scalar product[note 1] is an algebraic operation that takes two equal length sequences of numbers (usually coordinate vectors), and returns a single number. in euclidean geometry, the dot product of the cartesian coordinates of two vectors is widely used. it is often called the inner product (or rarely the. The dot product. 🔗. 🔗. in this section, we introduce a simple algebraic operation, known as the dot product, that helps us measure the length of vectors and the angle formed by a pair of vectors. for two dimensional vectors v and , w, their dot product v ⋅ w is the scalar defined to be. . v ⋅ w = [v 1 v 2] ⋅ [w 1 w 2] = v 1 w 1 v.
Dot Product Of Two Vectors Youtube In mathematics, the dot product or scalar product[note 1] is an algebraic operation that takes two equal length sequences of numbers (usually coordinate vectors), and returns a single number. in euclidean geometry, the dot product of the cartesian coordinates of two vectors is widely used. it is often called the inner product (or rarely the. The dot product. 🔗. 🔗. in this section, we introduce a simple algebraic operation, known as the dot product, that helps us measure the length of vectors and the angle formed by a pair of vectors. for two dimensional vectors v and , w, their dot product v ⋅ w is the scalar defined to be. . v ⋅ w = [v 1 v 2] ⋅ [w 1 w 2] = v 1 w 1 v. There are two ways in which we calculate the product of two vectors, these are known as the dot product and the cross product. 3.6.1. dot product #. definition 3.6 (the dot product) the dot product (also known as the scalar product) of two vectors a and b in r n, is defined by. (3.3) # a ⋅ b = ∑ i = 1 n a i b i = a 1 b 1 a 2 b 2 ⋯ a. Learn about the dot product and how it measures the relative direction of two vectors. cross products. matrices, intro.
Comments are closed.