Equation Of Motion Of Simple Pendulum Using Hamiltons Equation Of Motion Classical Mechanics

Equation Of Motion Of Simple Pendulum Using Hamilton S Equation Classical mechanics this video helps to understand the equation of motion derivation using hamilton's equation of motion. University of victoria. in classical mechanics we can describe the state of a system by specifying its lagrangian as a function of the coordinates and their time rates of change: l = l(qi,q˙) (14.3.1) if the coordinates and the velocities increase, the corresponding increment in the lagrangian is. dl = ∑i ∂l ∂qi dqi ∑i ∂l ∂qi.

Equation Of Motion Of Simple Pendulum Using Hamilton S Equation Of This lecture speaks about the derivation of the equation of motion for a simple pendulum using hamiltonian dynamics. the time period is also elucidated at th. The equations of motion of a system can be derived using the hamiltonian coupled with hamilton’s equations of motion, that is, equations \((8.3.11 8.3.13)\). formally the hamiltonian is constructed from the lagrangian. that is. select a set of independent generalized coordinates \(q {i}\) partition the active forces. H = p2 2mr2 mgr(1 − cos θ) h = p 2 2 m r 2 m g r (1 − cos. ⁡. θ) now hamilton's equations will be: p˙ = −mgr sin θ p ˙ = − m g r sin θ. θ˙ = p mr2 θ ˙ = p m r 2. i know one of the points of hamiltonian formalism is to get first order diff. equations instead of second order that lagrangian formalism gives you, but how can. Another example in using the hamilton jacobi method (t dependent h) (g 10.8) suppose we are given a hamiltonian to a system as, 2 2 p h matq m where a is a constant tq pmv 0, 0, 000 our task is to solve for the equation of motion by means of the hamilton’s principle function s with the initial conditions the hamilton jacobi equation for s is:.

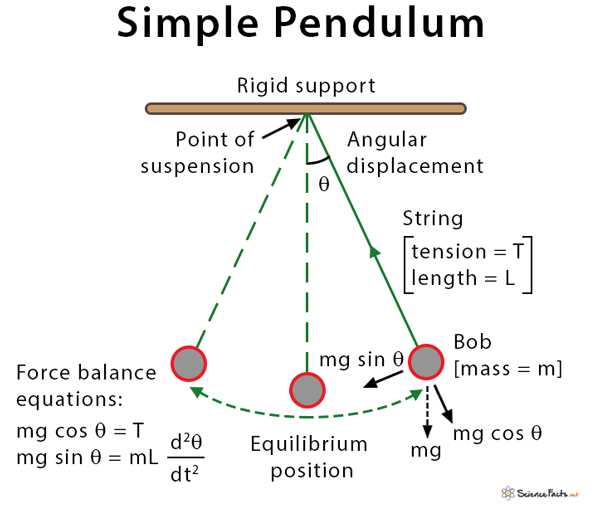
Simple Pendulum Equation H = p2 2mr2 mgr(1 − cos θ) h = p 2 2 m r 2 m g r (1 − cos. ⁡. θ) now hamilton's equations will be: p˙ = −mgr sin θ p ˙ = − m g r sin θ. θ˙ = p mr2 θ ˙ = p m r 2. i know one of the points of hamiltonian formalism is to get first order diff. equations instead of second order that lagrangian formalism gives you, but how can. Another example in using the hamilton jacobi method (t dependent h) (g 10.8) suppose we are given a hamiltonian to a system as, 2 2 p h matq m where a is a constant tq pmv 0, 0, 000 our task is to solve for the equation of motion by means of the hamilton’s principle function s with the initial conditions the hamilton jacobi equation for s is:. Appropriate for application to statistical mechanics and quantum mechanics newtonian and lagrangian viewpoints take the . q. i. as the fundamental variables • n variable configuration space • appears only as a convenient shorthand for dq dt • working formulas are 2nd order differential equations. Obtain the lagrangian and equation of motion of the bead. (4) consider a system of two identical pendulums of unit length and unit mass in a gravitational field g. suppose the pendulums are connected by a weightless spring of spring constant k. assuming simple harmonic motion, obtain equations of motion of the system.

Ppt Simple Pendulum Powerpoint Presentation Free Download Id 814485 Appropriate for application to statistical mechanics and quantum mechanics newtonian and lagrangian viewpoints take the . q. i. as the fundamental variables • n variable configuration space • appears only as a convenient shorthand for dq dt • working formulas are 2nd order differential equations. Obtain the lagrangian and equation of motion of the bead. (4) consider a system of two identical pendulums of unit length and unit mass in a gravitational field g. suppose the pendulums are connected by a weightless spring of spring constant k. assuming simple harmonic motion, obtain equations of motion of the system.

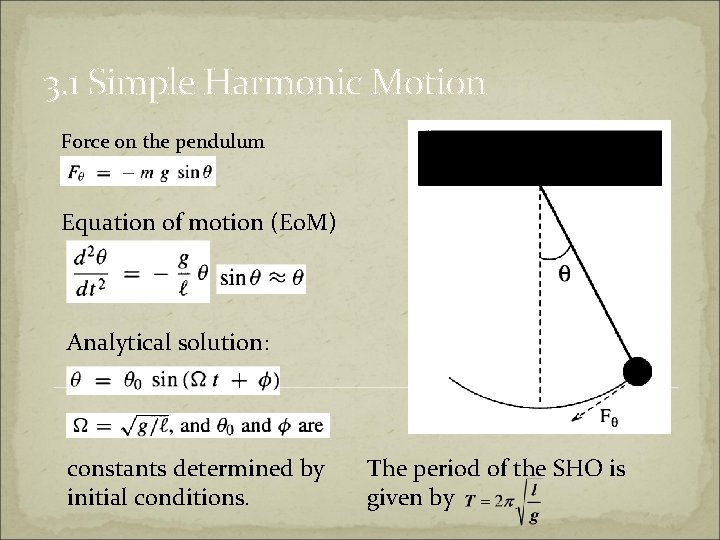
Simple Pendulum Equation