Equation Of Pair Of Tangent From An External Point To A Circle

Equation Of Pair Of Tangent From An External Point To A Circle Given a circle $c(x,y) \\equiv x^2 y^2 2gx 2fy c=0$ and a point $p = (x 1,y 1)$ outside the circle, the equation of the pair of straight lines that are tangent to. So, to convert the unit circle tangent lines into the original coordinate system, apply the three transformations in reverse order, i.e., if m = rst is the transformation that maps points into the unit circle’s coordinate system, then the tangents are lm = [1: ∓ √d2 − 1: d]rst. for the circle (x − h)2 (y − k)2 = r2 and point p.

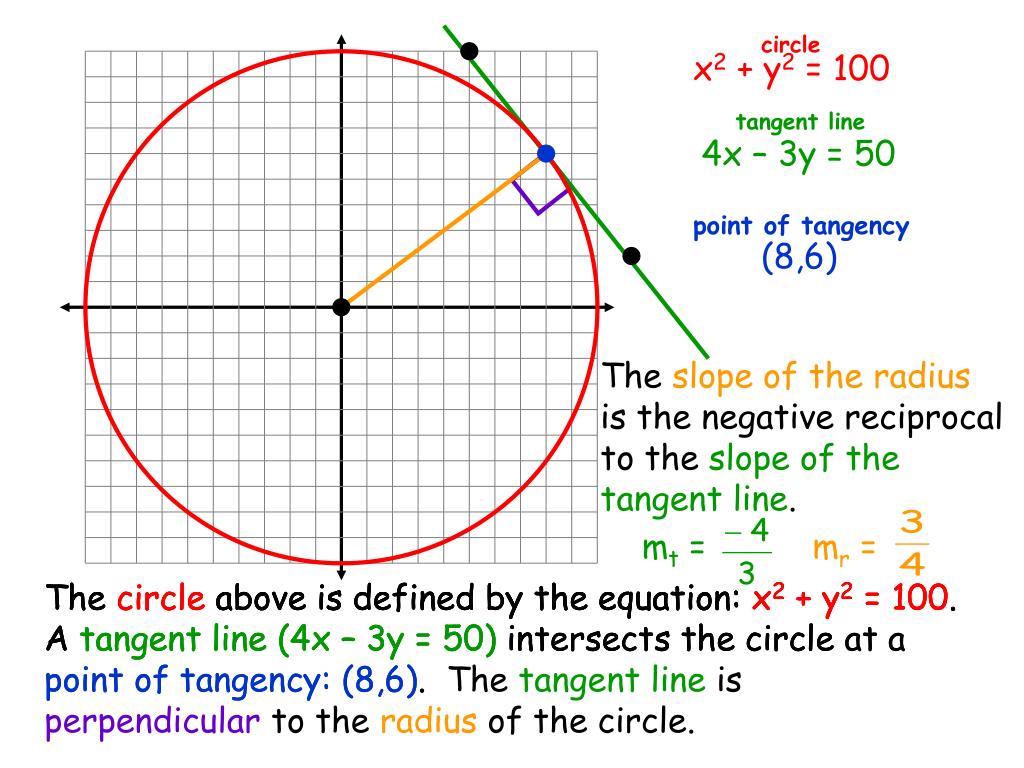
Ppt Equation Of Tangent Line Powerpoint Presentation Free Download The tangent to a circle equation x 2 y 2 2gx 2fy c =0 at (x 1, y 1) is the length of tangents from an external point to a circle are equal. tangent formula. The following figure shows a circle s and a point p external to s. a tangent from p has been drawn to s. this is an example of a tangent from an external point: how many tangents do you think can be drawn from an external point to a circle? the answer is two, and the following theorem proves this fact. theorem: exactly two tangents can be drawn. Equation of the chord joining two points (acosθ, a sinθ) and (acosφ, asinφ) on the circle x2 y2 = a2 is . x cos. note that in case θ → φ it becomes a tangent given by. xcosφ y sinφ = a. external and internal contacts of circles. two circles with centers c1(x 1, y 1) and c 2 (x 2, y 2) and radii r 1, r 2 respectively touch each. In euclidean plane geometry, a tangent line to a circle is a line that touches the circle at exactly one point, never entering the circle's interior. tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs. since the tangent line to a circle at a point p is.

Tangent Circle Formula Learn The Formula Of Tangent Circle Along With Equation of the chord joining two points (acosθ, a sinθ) and (acosφ, asinφ) on the circle x2 y2 = a2 is . x cos. note that in case θ → φ it becomes a tangent given by. xcosφ y sinφ = a. external and internal contacts of circles. two circles with centers c1(x 1, y 1) and c 2 (x 2, y 2) and radii r 1, r 2 respectively touch each. In euclidean plane geometry, a tangent line to a circle is a line that touches the circle at exactly one point, never entering the circle's interior. tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs. since the tangent line to a circle at a point p is. Remove parentheses and subtract 360 from both sides: –2∠mjp –2∠ojm = –180. divide through by –2:: ∠mjp ∠ojm = 90. 8. jp is a tangent to circle o and passes through p. jp is a tangent to o because it touches the circle at j and is at right angles to a radius at the contact point. (see tangent to a circle.). Equation of pair of tangents to a circle. let the equation of circle s = x2 x 2 y2 y 2 – a2 a 2 and p (x1,y1 x 1, y 1) is any point outside the circle. from the point we can draw two real and distinct tangent and combine equation of pair of tangents is –. (x2 x 2 y2 y 2 – a2 a 2) (x12 x 1 2 y12 y 1 2 – a2 a 2) = (xx1 yy1–a2)2.

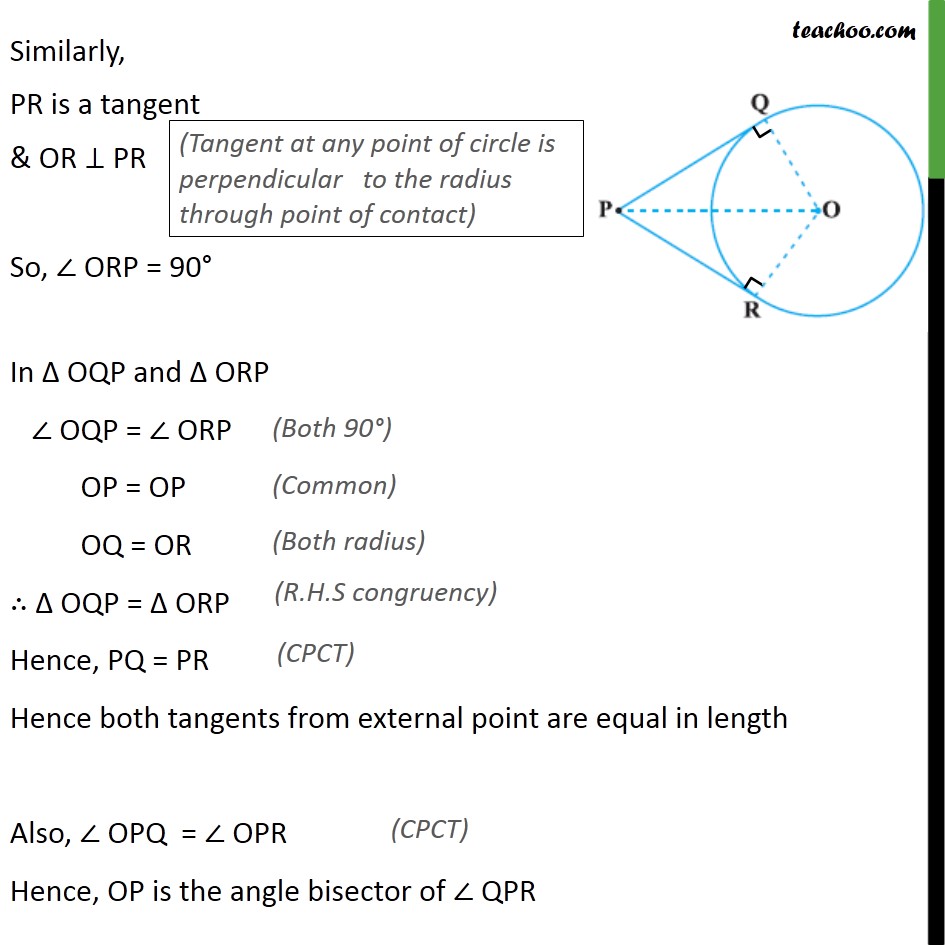
Theorem 10 2 Class 10 Tangents From External Point Of Circle Are Remove parentheses and subtract 360 from both sides: –2∠mjp –2∠ojm = –180. divide through by –2:: ∠mjp ∠ojm = 90. 8. jp is a tangent to circle o and passes through p. jp is a tangent to o because it touches the circle at j and is at right angles to a radius at the contact point. (see tangent to a circle.). Equation of pair of tangents to a circle. let the equation of circle s = x2 x 2 y2 y 2 – a2 a 2 and p (x1,y1 x 1, y 1) is any point outside the circle. from the point we can draw two real and distinct tangent and combine equation of pair of tangents is –. (x2 x 2 y2 y 2 – a2 a 2) (x12 x 1 2 y12 y 1 2 – a2 a 2) = (xx1 yy1–a2)2.