Equilateral Triangles Inscribed In A Square

Two Equilateral Triangles On Sides Of A Square The equilateral triangle is also the only triangle that can have both rational side lengths and angles (when measured in degrees). when inscribed in a unit square, the maximal possible area of an equilateral triangle is \(2\sqrt{3} 3\), occurring when the triangle is oriented at a \(15^{\circ}\) angle and has sides of length \(\sqrt{6} \sqrt{2}:\). $\begingroup$ @handebruijn because if you choose any square inside the triangle that does not fit the definition that i gave, an equilateral triangle of smallest area which covers this square will have less area than the first equilateral triangle. in the other words, try to draw an equiateral triangle of smallest area which covers a square.

Equilateral Triangle Inscribed In A Unit Square What Is The Area Of Let the side of the equilateral triangle be s = ae = ef = af. triangles abe and afd are congruent. this is because they are both right triangles whose hypotenuse is s and longer leg is 1. by the gougu theorem (aka pythagorean theorem), the remaining leg in each triangle has length described by: df = be = x s 2 = 1 2 x 2 s 2 = 1 x 2. we then. To begin, consider an equilateral triangle. the geom etry is shown in figure 1 and has been augmented with various properties explained below. for students, constructing diagrams using dynamic geometry soft ware provides a starting point for thinking about the location of the square. for this diagram, the equilateral triangle, abc,. H = a × √3 2. substituting h into the first area formula, we obtain the equation for the equilateral triangle area: area = a² × √3 4. 2. using trigonometry. let's start with the trigonometric triangle area formula: area = (1 2) × a × b × sin(γ), where γ is the angle between the sides. we remember that all sides and all angles. That is, consider (construct) any other inscribed equilateral triangle. will it cover more, the same, or less of the area? for example, see the second figure at the right. make a gsp construction. prove that the first example shows the maximum area of an equilateral triangle inscribed in a square.

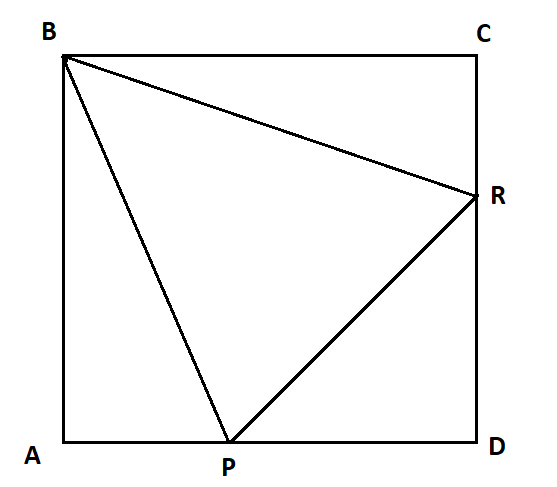
Fold Square Into Equilateral Triangle H = a × √3 2. substituting h into the first area formula, we obtain the equation for the equilateral triangle area: area = a² × √3 4. 2. using trigonometry. let's start with the trigonometric triangle area formula: area = (1 2) × a × b × sin(γ), where γ is the angle between the sides. we remember that all sides and all angles. That is, consider (construct) any other inscribed equilateral triangle. will it cover more, the same, or less of the area? for example, see the second figure at the right. make a gsp construction. prove that the first example shows the maximum area of an equilateral triangle inscribed in a square. Inscribe an equilateral triangle in a square . determine a construction to inscribe an equilateral triangle in a square as in figure 1. make a gsp construction. figure 1 . is this the inscribed equilateral triangle that has the maximum proportion of the area of the square? that is, consider (construct) any other inscribed equilateral triangle. An equilateral triangle is a triangle with all three sides of equal length a, corresponding to what could also be known as a "regular" triangle. an equilateral triangle is therefore a special case of an isosceles triangle having not just two, but all three sides equal. an equilateral triangle also has three equal 60 degrees angles. the altitude h of an equilateral triangle is h=asin60 degrees.

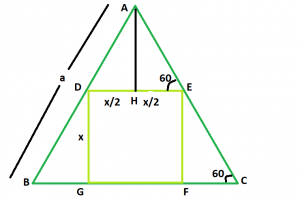
Biggest Square That Can Be Inscribed Within An Equilateral Triangle Inscribe an equilateral triangle in a square . determine a construction to inscribe an equilateral triangle in a square as in figure 1. make a gsp construction. figure 1 . is this the inscribed equilateral triangle that has the maximum proportion of the area of the square? that is, consider (construct) any other inscribed equilateral triangle. An equilateral triangle is a triangle with all three sides of equal length a, corresponding to what could also be known as a "regular" triangle. an equilateral triangle is therefore a special case of an isosceles triangle having not just two, but all three sides equal. an equilateral triangle also has three equal 60 degrees angles. the altitude h of an equilateral triangle is h=asin60 degrees.