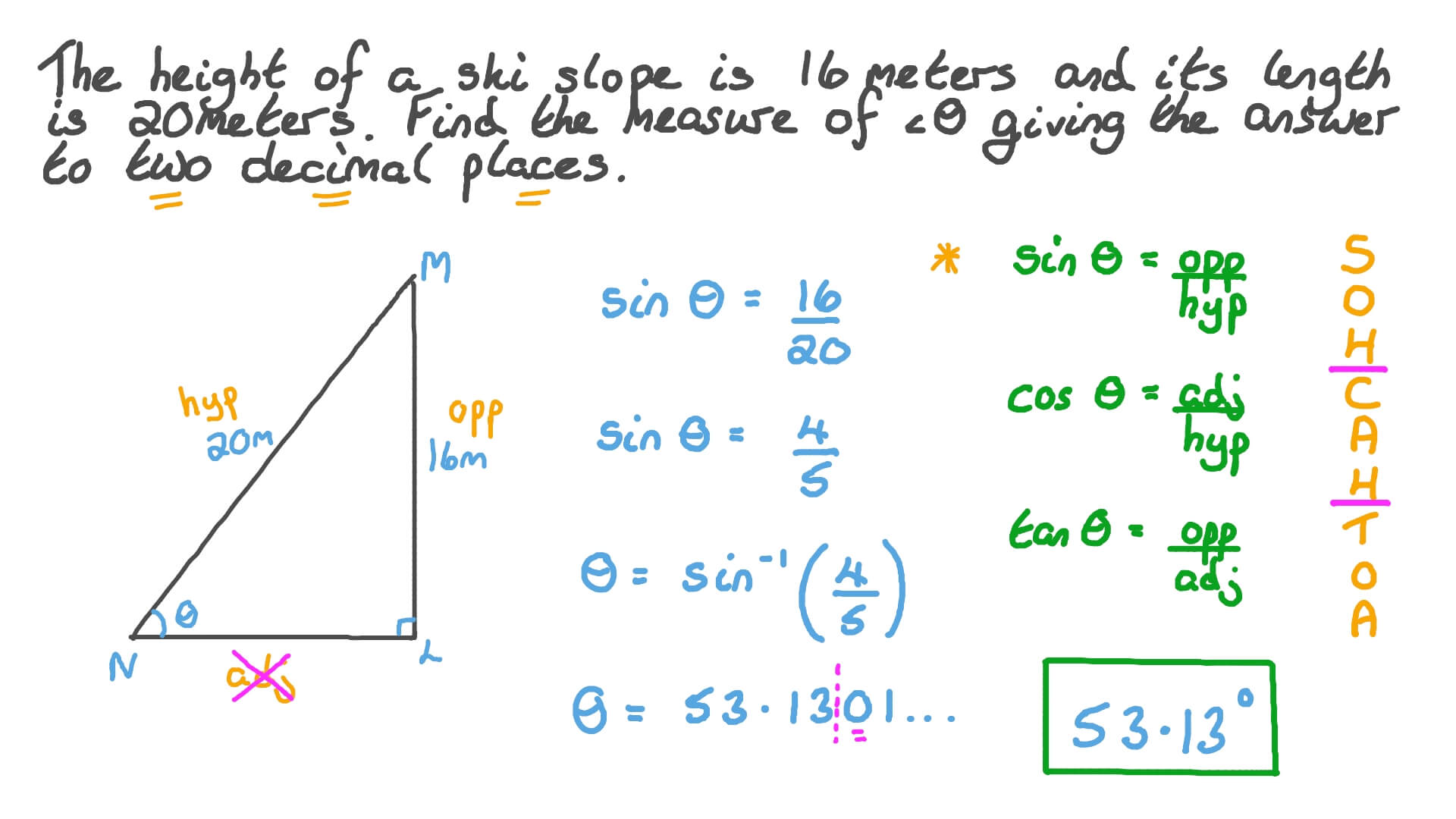
Example Determine The Measure Of An Angle Of A Right Triangle Using A This video provides examples of determining the measure of an angle of a right triangle with the length of two side given plete video lists at mathisp. To solve a right triangle using trigonometry: identify an acute angle in the triangle α. for this angle: sin(α) = opposite hypotenuse; and. cos(α) = adjacent hypotenuse. by taking the inverse trigonometric functions, we can find the value of the angle α. you can repeat the procedure for the other angle.
Using Trigonometric Ratios To Solve For An Angle Of A Right Triangle Example. find the size of angle a°. step 1 the two sides we know are a djacent (6,750) and h ypotenuse (8,100). step 2 soh cah toa tells us we must use c osine. step 3 calculate adjacent hypotenuse = 6,750 8,100 = 0.8333. step 4 find the angle from your calculator using cos 1 of 0.8333: cos a° = 6,750 8,100 = 0.8333. For example, the area of a right triangle is equal to 28 in² and b = 9 in. our right triangle side and angle calculator displays missing sides and angles! now we know that: a = 6.222 in; c = 10.941 in; α = 34.66° β = 55.34° now, let's check how finding the angles of a right triangle works: refresh the calculator. pick the option you need. It’s a mnemonic device to help you remember the three basic trig ratios used to solve for missing sides and angles in a right triangle. it’s defined as: soh: sin (θ) = opposite hypotenuse. cah: cos (θ) = adjacent hypotenuse. toa: tan (θ) = opposite adjacent. The 45° 45° 90° triangle, also referred to as an isosceles right triangle, since it has two sides of equal lengths, is a right triangle in which the sides corresponding to the angles, 45° 45° 90°, follow a ratio of 1:1:√ 2. like the 30° 60° 90° triangle, knowing one side length allows you to determine the lengths of the other sides.
Right Triangle Trigonometry Lesson 4f4 It’s a mnemonic device to help you remember the three basic trig ratios used to solve for missing sides and angles in a right triangle. it’s defined as: soh: sin (θ) = opposite hypotenuse. cah: cos (θ) = adjacent hypotenuse. toa: tan (θ) = opposite adjacent. The 45° 45° 90° triangle, also referred to as an isosceles right triangle, since it has two sides of equal lengths, is a right triangle in which the sides corresponding to the angles, 45° 45° 90°, follow a ratio of 1:1:√ 2. like the 30° 60° 90° triangle, knowing one side length allows you to determine the lengths of the other sides. Right triangle trigonometry. the word trigonometry can be broken into the parts tri, gon, and metry, which means “three angle measurement,” or equivalently “triangle measurement.”. throughout this unit, we will learn new ways of finding missing sides and angles of triangles which we would be unable to find using the pythagorean theorem. θ = sin 1(o h). the formula for finding a missing angle using sine. for example, calculate the missing angle on the right angled triangle shown. the opposite side is 5 cm long and the hypotenuse is 9 cm long. we substitute the values of o = 5 and h = 9 into the equation to obtain .
Example Determine The Length Of A Side Of A Right Triangle Using A Right triangle trigonometry. the word trigonometry can be broken into the parts tri, gon, and metry, which means “three angle measurement,” or equivalently “triangle measurement.”. throughout this unit, we will learn new ways of finding missing sides and angles of triangles which we would be unable to find using the pythagorean theorem. θ = sin 1(o h). the formula for finding a missing angle using sine. for example, calculate the missing angle on the right angled triangle shown. the opposite side is 5 cm long and the hypotenuse is 9 cm long. we substitute the values of o = 5 and h = 9 into the equation to obtain .
Comments are closed.