Factorisation Of Algebric Expression Using Identity A Square B Square Factorization by using identities will help us to factorize an algebraic expression easily. the following identities are: (i) (a b) 2 = a 2 2ab b 2, (ii) (a b) 2 = a 2 2ab b 2 and. (iii) a 2 – b 2 = (a b) (a – b). now we will use these identities to factorize the given algebraic expressions. solved examples on factorization by. Some standard algebraic identities list are given below: identity i: (a b) 2 = a 2 2ab b 2. identity ii: (a – b) 2 = a 2 – 2ab b 2. identity iii: a 2 – b 2 = (a b) (a – b) identity iv: (x a) (x b) = x 2 (a b) x ab. identity v: (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2ca.
Factoring Formulas In Algebra What Are Factoring Formulas Worksheet 2:6 factorizing algebraic expressions section 1 finding factors factorizing algebraic expressions is a way of turning a sum of terms into a product of smaller ones. the product is a multiplication of the factors. sometimes it helps to look at a simpler case before venturing into the abstract. the number 48 may be written as a product in a. An example of algebra expression is (a b) 2 = a 2 2ab b 2, and an example of algebraic expression is ax 2 bx c. how can we verify an algebra identity? the algebra identities can be easily verified in two ways. one is by substituting the values in places of the variables within the algebraic identities. Algebraic identity definition. an important set of mathematical formulas or equations where the value of the l.h.s. of the equation is equal to the value of the r.h.s. of the equation. algebraic identities simplify algebraic expressions and calculations. here are examples of common algebraic identities: $(a b)^2 = a^2 2ab b^2$. Factorization of algebraic expressions using common factor method. follow the steps given below to find the factors of the expression: x2 4x x 2 4 x. step 1: x2 x 2 can be factorized as x×x x × x, and 4x 4 x can be factorized as x×2×x x × 2 × x. step 2: find the greatest common factor of the two terms. here, we see that x x is the.
3 Manières De Factoriser Des équations Algébriques Algebraic identity definition. an important set of mathematical formulas or equations where the value of the l.h.s. of the equation is equal to the value of the r.h.s. of the equation. algebraic identities simplify algebraic expressions and calculations. here are examples of common algebraic identities: $(a b)^2 = a^2 2ab b^2$. Factorization of algebraic expressions using common factor method. follow the steps given below to find the factors of the expression: x2 4x x 2 4 x. step 1: x2 x 2 can be factorized as x×x x × x, and 4x 4 x can be factorized as x×2×x x × 2 × x. step 2: find the greatest common factor of the two terms. here, we see that x x is the. The last step uses identities to find the factors for the given expression. since the lhs for the identity a 2 2ab b 2 is (a b) 2 we write the factors using the identity as: (3x 6) 2 = (3x 6) (3x 6). so the factor for 9x 2 –18 x 36 is (3x 6) (3x 6). learn more about factorisation using division. solved examples for you. Factoring: finding what to multiply together to get an expression. it is like "splitting" an expression into a multiplication of simpler expressions. example: factor 2y 6. both 2y and 6 have a common factor of 2: 2y is 2×y. 6 is 2×3. so we can factor the whole expression into: 2y 6 = 2 (y 3).
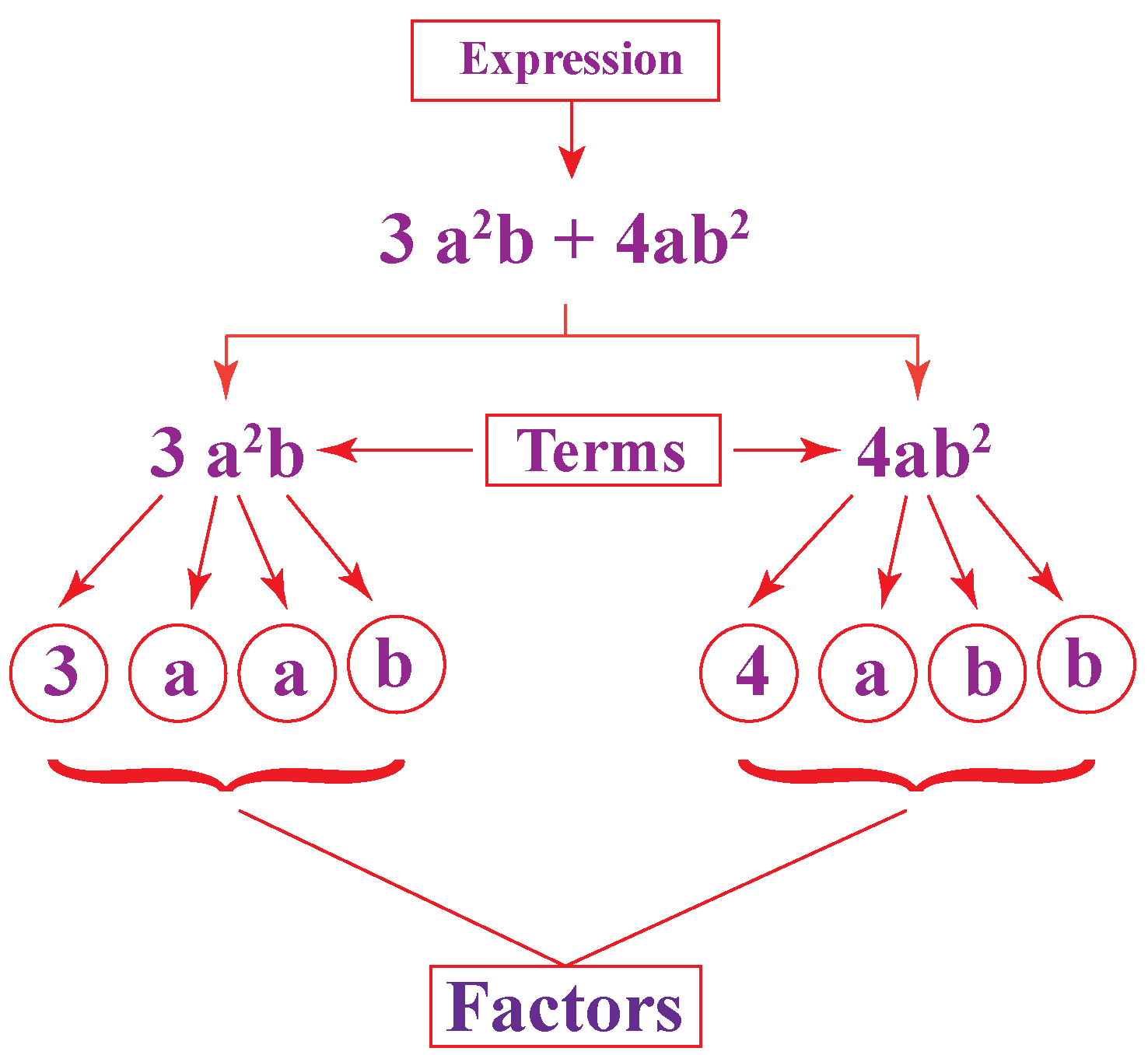
Factorization Of Algebraic Expressions Identities Examples Cuemath The last step uses identities to find the factors for the given expression. since the lhs for the identity a 2 2ab b 2 is (a b) 2 we write the factors using the identity as: (3x 6) 2 = (3x 6) (3x 6). so the factor for 9x 2 –18 x 36 is (3x 6) (3x 6). learn more about factorisation using division. solved examples for you. Factoring: finding what to multiply together to get an expression. it is like "splitting" an expression into a multiplication of simpler expressions. example: factor 2y 6. both 2y and 6 have a common factor of 2: 2y is 2×y. 6 is 2×3. so we can factor the whole expression into: 2y 6 = 2 (y 3).
Comments are closed.