Find Angle Between Two Vectors If Cross Product And Dot

Find Angle Between Two Vectors If Cross Product And Dot Product Are If we have v x w = <2, 1, 1> (cross product) and v ⋅ w = 4, (dot product) is it possible to find the angle between vectors v and w? note that i do not actually know values for the vectors, just their products. i was under the impression that i had to know the norms of the vectors to find the angle. is this not the case? thanks. On most calculators, use either the arccos or cos 1 function on your calculator to find the angle θ. simply enter “arccos” and the dot product divided by the vectors’ magnitudes. for some results, use the unit circle to work out the angle. finding an angle with cosine. in our example, θ = cos 1 (√2 2).

Angle Between Two Vectors Formula How To Find Formula to find the angle θ between the two vectors 'a' and 'b' using cross product : example 1 : find the angle between the following two vectors using cross product. Example 1. earlier, you were asked to find the dot product between the two vectors and . it can be computed as: the result of zero makes sense because these two vectors are perpendicular to each other. example 2. find the dot product between the following vectors: example 3. prove the angle between two vectors formula:. Let us see some examples of finding the angle between two vectors using dot product in both 2d and 3d. let us also see the ambiguity caused by the cross product formula to find the angle between two vectors. angle between two vectors in 2d. let us consider two vectors in 2d say a = <1, 2> and b = < 2, 1>. let θ be the angle between them. Using the dot product to find the angle between two vectors. when two nonzero vectors are placed in standard position, whether in two dimensions or three dimensions, they form an angle between them (figure 2.44). the dot product provides a way to find the measure of this angle.

Using Dot Product To Find The Angle Between Two Vectors Youtube Let us see some examples of finding the angle between two vectors using dot product in both 2d and 3d. let us also see the ambiguity caused by the cross product formula to find the angle between two vectors. angle between two vectors in 2d. let us consider two vectors in 2d say a = <1, 2> and b = < 2, 1>. let θ be the angle between them. Using the dot product to find the angle between two vectors. when two nonzero vectors are placed in standard position, whether in two dimensions or three dimensions, they form an angle between them (figure 2.44). the dot product provides a way to find the measure of this angle. $\begingroup$ yes, once one has the value of $\sin \theta$ in hand, (if it is not equal to $1$) one needs to decide whether the angle is more or less than $\frac{\pi}{2}$, which one can do using, e.g., the dot product. To calculate the angle between two vectors in a 3d space: find the dot product of the vectors. divide the dot product by the magnitude of the first vector. divide the resultant by the magnitude of the second vector. mathematically, angle α between two vectors [xa, ya, za] and [xb, yb, zb] can be written as:.

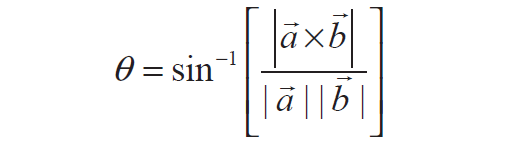
Angle Between Two Vectors Using Cross Product $\begingroup$ yes, once one has the value of $\sin \theta$ in hand, (if it is not equal to $1$) one needs to decide whether the angle is more or less than $\frac{\pi}{2}$, which one can do using, e.g., the dot product. To calculate the angle between two vectors in a 3d space: find the dot product of the vectors. divide the dot product by the magnitude of the first vector. divide the resultant by the magnitude of the second vector. mathematically, angle α between two vectors [xa, ya, za] and [xb, yb, zb] can be written as:.