Find The Area Of A Shaded Square Inside Of A Triangle Step By Step

Find The Area Of A Shaded Square Inside Of A Triangle Step By Step Can you find the area of the shaded square efgh? use the corresponding angles postulate and the angle angle angle theorem (aaa). quick and easy explanation b. A smaller square = s 2. a smaller square = 5 x 5. a smaller square = 25 square meters. find the area of the shaded region by subtracting the obtained area of the smaller square from the area measurement of the larger square shape. a shaded region = a bigger square a smaller square. a shaded region = 36 25.

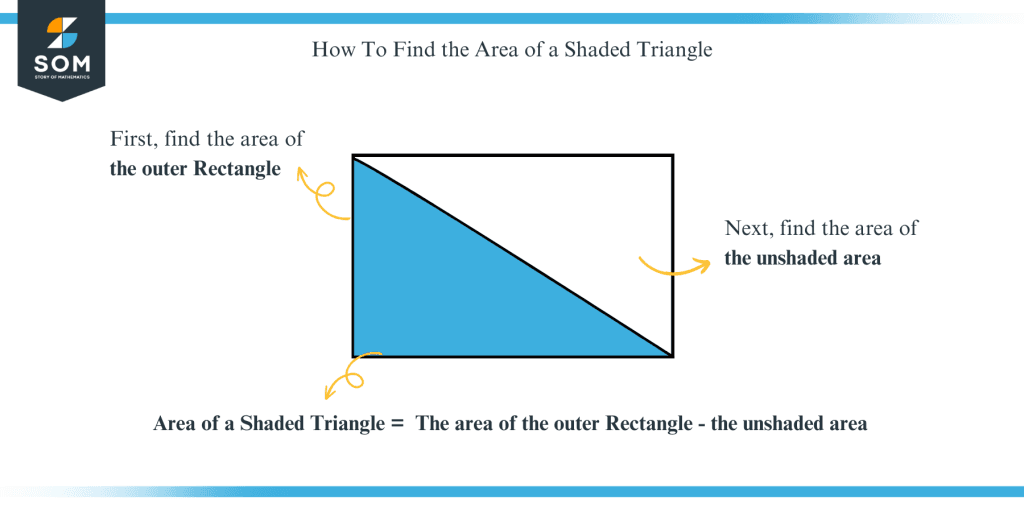
Can You Calculate The Area Of A Triangle That Is Inside Of A Square Scroll down the page for more examples and solutions. step 1: find area of inner shape. step 2: find area of outer shape. step 3: area of shaded region = area of outer shape – area of inner shape. example 2: find the area of the shaded region: solution: step 1: find area of inner square = 2 cm × 2 cm = 4 cm 2. step 2: find area of outer. To find the area of the shaded region, you need to first find the total area of the rectangle. then find the area of the triangle. instead of adding the areas together, here you will be subtracting the areas. area of a\text{: } 7 \times 11=77 . area of b\text{: } \cfrac{1}{2} \, (4 \times 3)=6. Find the area of the shaded regions. (use π = \(\frac{22}{7}\)) solution: the given combined shape is combination of a triangle and incircle. to find the area of the shaded region of the given combined geometrical shape, subtract the area of the incircle (smaller geometrical shape) from the area of the ∆pqr (larger geometrical shape). Area of square (gehf) = 36 cm 2. area of shaded region = 320 36 = 284 cm 2. example 3 : find the area of the shaded portion. solution : to find the area of shaded region, we have to subtract area of semicircle with diameter cb from area of semicircle with diameter ab and add the area of semicircle of diameter ac.

Find Area Of Shaded Triangle Triangle And Semicircle Are Inscribed In Find the area of the shaded regions. (use π = \(\frac{22}{7}\)) solution: the given combined shape is combination of a triangle and incircle. to find the area of the shaded region of the given combined geometrical shape, subtract the area of the incircle (smaller geometrical shape) from the area of the ∆pqr (larger geometrical shape). Area of square (gehf) = 36 cm 2. area of shaded region = 320 36 = 284 cm 2. example 3 : find the area of the shaded portion. solution : to find the area of shaded region, we have to subtract area of semicircle with diameter cb from area of semicircle with diameter ab and add the area of semicircle of diameter ac. Shaded area formula: if you want to calculate the shaded area by hand, you need to subject to the following equation: shaded area = l^ {2} \pi * \left (\dfrac {l} {2}\right)^ {2} s hadedarea = l2 −π ∗ (2l)2. where; l = diameter or length of circle or square. let us resolve an example to make your concept more clear regarding shaded area. For such cases, it is often possible to calculate the area of the desired shape by calculating the area of the outer shape, and then subtracting the areas of the inner shapes. tip: when asked to find the "shaded" region, that is often a hint to use this approach as in another problem we've solved. in this problem, it is easy to find the area.

How To Find The Area Of The Shaded Region Triangle In A Square Math Shaded area formula: if you want to calculate the shaded area by hand, you need to subject to the following equation: shaded area = l^ {2} \pi * \left (\dfrac {l} {2}\right)^ {2} s hadedarea = l2 −π ∗ (2l)2. where; l = diameter or length of circle or square. let us resolve an example to make your concept more clear regarding shaded area. For such cases, it is often possible to calculate the area of the desired shape by calculating the area of the outer shape, and then subtracting the areas of the inner shapes. tip: when asked to find the "shaded" region, that is often a hint to use this approach as in another problem we've solved. in this problem, it is easy to find the area.

Area Of A Shaded Triangle A Complete Guide The Story Of Mathematics