Finding The Area Under The Curve Using Definite Integrals Calculus

Integral Calculus Lesson 4 How To Find The Area Under A Curve Figure 6.1.2: (a)we can approximate the area between the graphs of two functions, f(x) and g(x), with rectangles. (b) the area of a typical rectangle goes from one curve to the other. the height of each individual rectangle is f(x ∗ i) − g(x ∗ i) and the width of each rectangle is Δx. adding the areas of all the rectangles, we see that. This calculus video tutorial explains how to find the area under the curve using definite integrals in terms of x and y.antiderivatives:.

Finding The Area Under The Curve Using Definite Integrals Calculus Section 6.2 : area between curves. determine the area below f (x) =3 2x −x2 f (x) = 3 2 x − x 2 and above the x axis. solution. determine the area to the left of g(y) =3 −y2 g (y) = 3 − y 2 and to the right of x =−1 x = − 1. solution. for problems 3 – 11 determine the area of the region bounded by the given set of curves. We use the right triangle with legs parallel to the coordinate axes and hypotenuse connecting the endpoints of the slice, as seen at right in figure 6.1.7. the length, h, of the hypotenuse approximates the length, lslice, of the curve between the two selected points. thus, lslice ≈ h = √(Δx)2 (Δy)2. Total area. one application of the definite integral is finding displacement when given a velocity function. if v (t) v (t) represents the velocity of an object as a function of time, then the area under the curve tells us how far the object is from its original position. this is a very important application of the definite integral, and we. In the limit, the definite integral equals area a1 a 1 minus area a2 a 2, or the net signed area. notice that net signed area can be positive, negative, or zero. if the area above the x x axis is larger, the net signed area is positive. if the area below the x x axis is larger, the net signed area is negative.

Finding Areas Between Two Curves Areas Of Plane Regions Using Total area. one application of the definite integral is finding displacement when given a velocity function. if v (t) v (t) represents the velocity of an object as a function of time, then the area under the curve tells us how far the object is from its original position. this is a very important application of the definite integral, and we. In the limit, the definite integral equals area a1 a 1 minus area a2 a 2, or the net signed area. notice that net signed area can be positive, negative, or zero. if the area above the x x axis is larger, the net signed area is positive. if the area below the x x axis is larger, the net signed area is negative. Figure 5.2.3: in the limit, the definite integral equals area a1 less area a2, or the net signed area. notice that net signed area can be positive, negative, or zero. if the area above the x axis is larger, the net signed area is positive. if the area below the x axis is larger, the net signed area is negative. Area under a curve from first principles. in the diagram above, a "typical rectangle" is shown with width `Δx` and height `y`. its area is `yΔx`. if we add all these typical rectangles, starting from `a` and finishing at `b`, the area is approximately: `sum {x=a}^\b(y)deltax` now if we let `Δx → 0`, we can find the exact area by integration:.
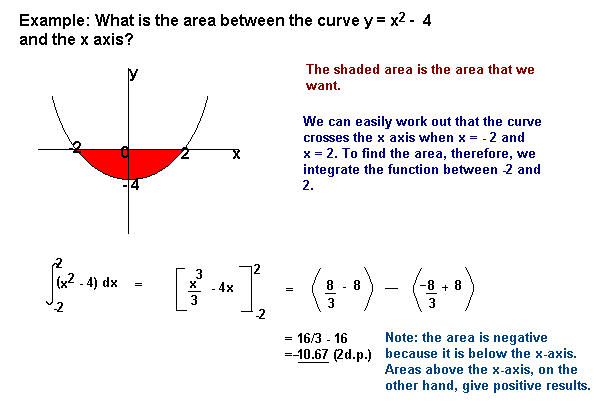
Area Under A Curve A2 Level Level Revision Maths Pure Mathematics Figure 5.2.3: in the limit, the definite integral equals area a1 less area a2, or the net signed area. notice that net signed area can be positive, negative, or zero. if the area above the x axis is larger, the net signed area is positive. if the area below the x axis is larger, the net signed area is negative. Area under a curve from first principles. in the diagram above, a "typical rectangle" is shown with width `Δx` and height `y`. its area is `yΔx`. if we add all these typical rectangles, starting from `a` and finishing at `b`, the area is approximately: `sum {x=a}^\b(y)deltax` now if we let `Δx → 0`, we can find the exact area by integration:.

Finding The Area Under A Curve Using Definite Integration Youtube

Comments are closed.