Golden Ratio Sign Logarithmic Spiral In Rectangle Fibonacci Sequence Nautilu

Golden Ratio Sign Logarithmic Spiral In Rectangle Nautilus Shell This resulting golden spiral is often associated with the nautilus spiral, but incorrectly because the two spirals are clearly very different. a golden spiral created from a golden rectangle expands in dimension by the golden ratio with every quarter, or 90 degree, turn of the spiral. this can be constructed by starting with a golden rectangle. An approximation of a logarithmic spiral, created by drawing circular arcs connecting the opposite corners of squares in the fibonacci tiling; this one uses squares of sizes 1, 1, 2, 3, 5, 8, 13.
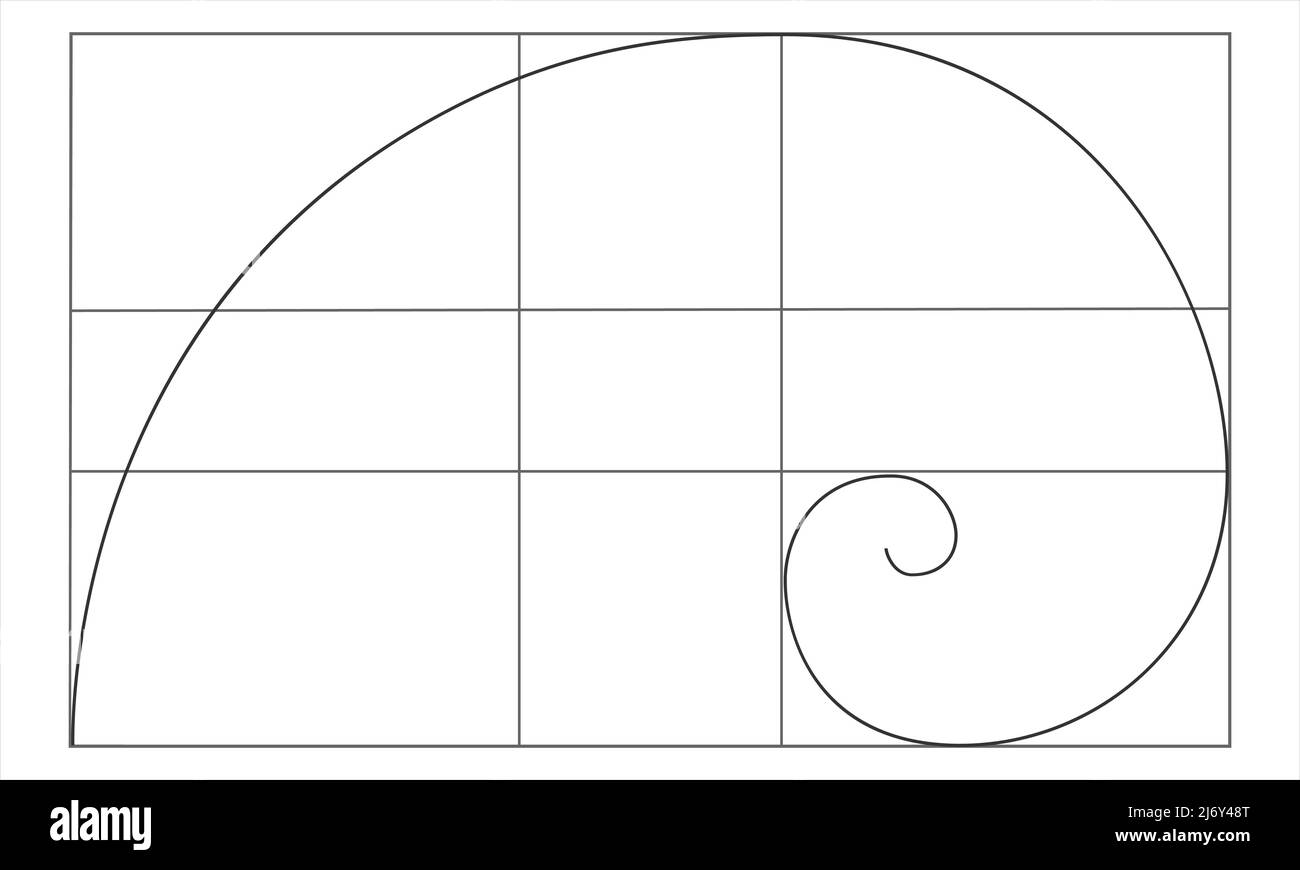
Golden Ratio Sign Logarithmic Spiral In Rectangle Fibonacci Sequence A rectangle in golden ratio proportions has the shorter side of 1 to the longer side of 1.618. this φ rectangle subdivides into a square and another golden ratio rectangle infinitely. an approximate logarithmic golden spiral is typically drawn in a golden rectangle or a similar rectangle using consecutive numbers from the fibonacci sequence. The fibonacci spiral gets closer and closer to a golden spiral as it increases in size because of the ratio of each number in the fibonacci series to the one before it converges on phi, 1.618, as the series progresses (e.g., 1, 1, 2, 3, 5, 8 and 13 produce ratios of 1, 2, 1.5, 1.67, 1.6 and 1.625, respectively) fibonacci spirals and golden. It is however, patterned on a logarithmic spiral (as is the golden spiral), but with a geometric ratio, on average, close to 1.31. phi (φ) is approximately 1.618. remarkably, one of the six known species of nautilus, the rare “crusty nautilus”, diverges in its proportions from the other five species, and demonstrates a geometric ratio of 1. Golden spiral. golden spirals are self similar. the shape is infinitely repeated when magnified. in geometry, a golden spiral is a logarithmic spiral whose growth factor is φ, the golden ratio. [1] that is, a golden spiral gets wider (or further from its origin) by a factor of φ for every quarter turn it makes.
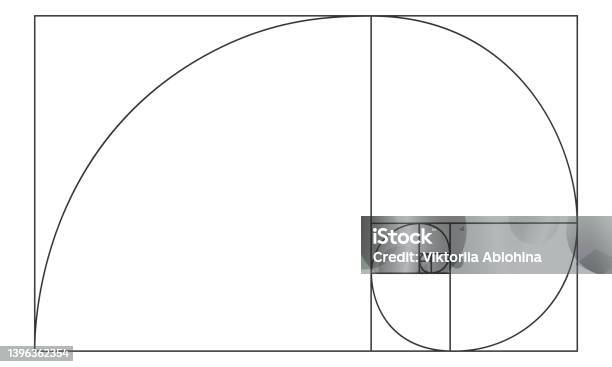
Golden Ratio Sign Logarithmic Spiral In Rectangle Nautilus Shell Shape It is however, patterned on a logarithmic spiral (as is the golden spiral), but with a geometric ratio, on average, close to 1.31. phi (φ) is approximately 1.618. remarkably, one of the six known species of nautilus, the rare “crusty nautilus”, diverges in its proportions from the other five species, and demonstrates a geometric ratio of 1. Golden spiral. golden spirals are self similar. the shape is infinitely repeated when magnified. in geometry, a golden spiral is a logarithmic spiral whose growth factor is φ, the golden ratio. [1] that is, a golden spiral gets wider (or further from its origin) by a factor of φ for every quarter turn it makes. The golden rectangle is a rectangle whose sides are fibonacci numbers, such as in the image below. for example, a = 8 and b = 5 , so that a b = 13 and the ratios yield: 1.6180339887498948420…. In this research, to compare the mean aspect ratio of nautilus shells to the 4:3 ratio and the meta golden ratio chi, eighty nautilus shells were measured in the smithsonian collection. the.
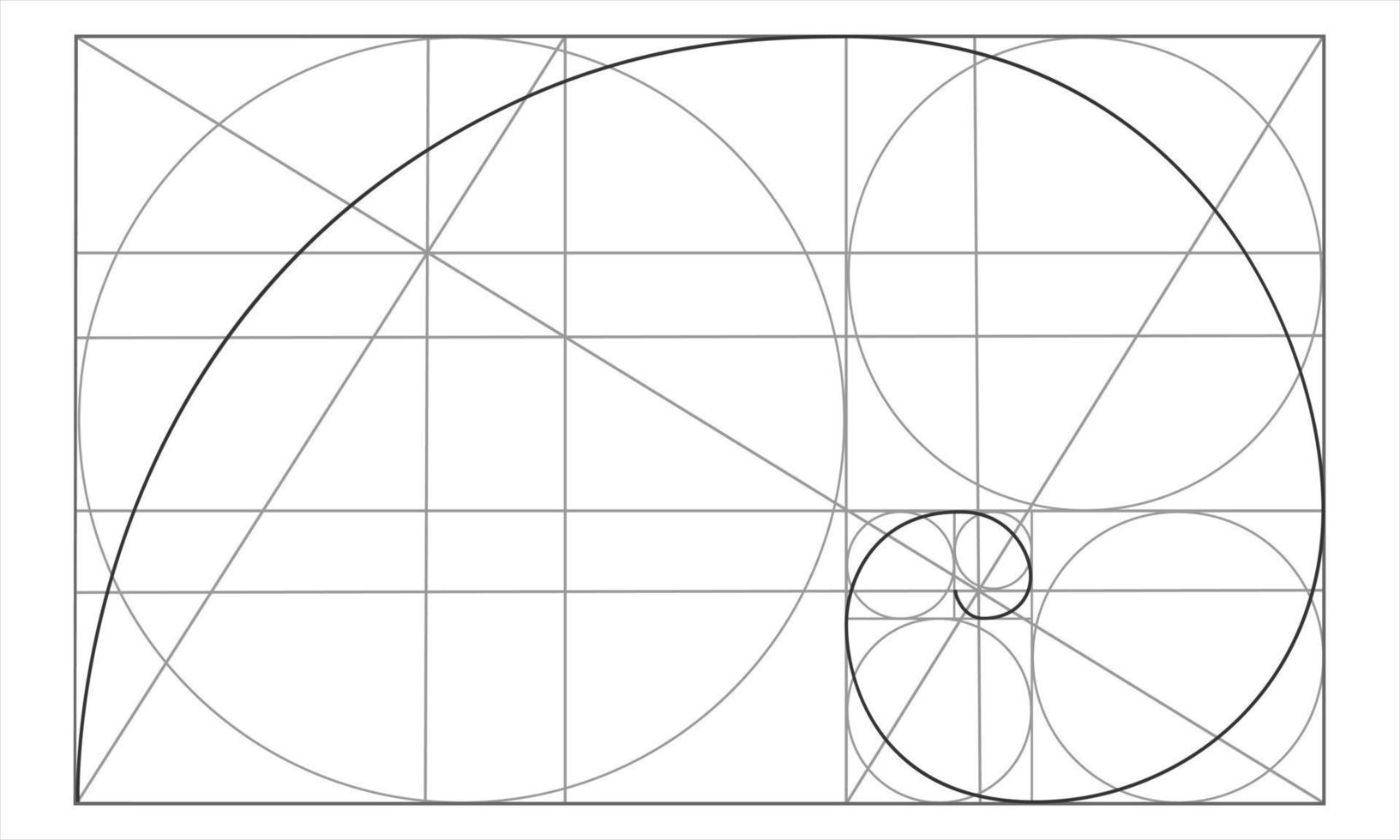
Golden Ratio Template Logarithmic Spiral In Rectangle With Circles And The golden rectangle is a rectangle whose sides are fibonacci numbers, such as in the image below. for example, a = 8 and b = 5 , so that a b = 13 and the ratios yield: 1.6180339887498948420…. In this research, to compare the mean aspect ratio of nautilus shells to the 4:3 ratio and the meta golden ratio chi, eighty nautilus shells were measured in the smithsonian collection. the.
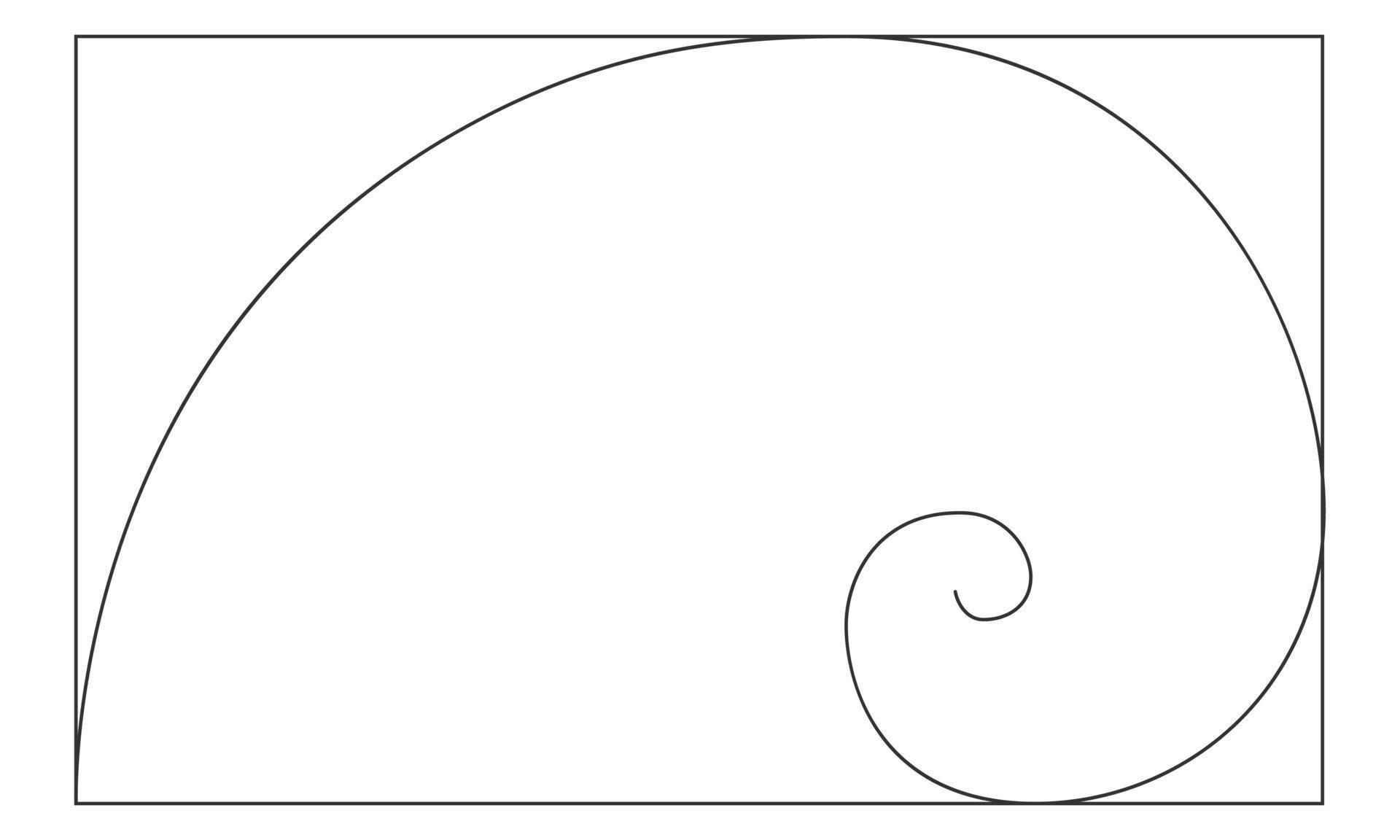
Golden Ratio Logarithmic Spiral In Rectangle Frame Harmony Nature

Comments are closed.