Grade 10 Proof For Midpoint Theorem Converse

By viagraultimate On Nov 10, 2024 Last updated

Gr 10 Geometry Triangles Midpoint Theorem And Converse Part 1 2 Statement: the converse of midpoint theorem states that "the line drawn through the midpoint of one side of a triangle that is parallel to another side will bisect the third side". we prove the converse of mid point theorem by contradiction. proof of mid point theorem converse. consider a triangle abc, and let d be the midpoint of ab. Q. prove the converse of the mid point theorem following the guidelines given below: consider a triangle abc with d as the mid point of ab. draw de∥bc to intersect ac in e. let e1 be the mid point of ac. use mid point theorem to get de1 ∥bc and de1=bc 2. conclude e=e1 and hence e is the mid point of ac.

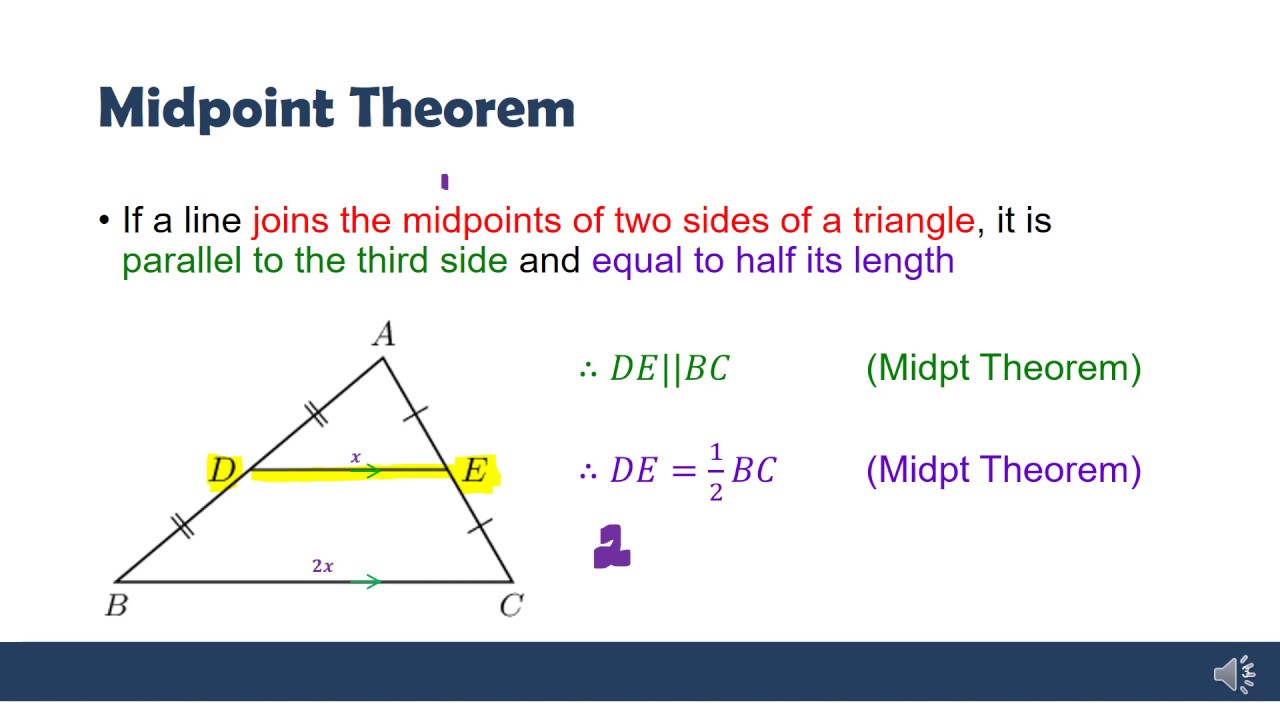
Converse Of Mid Point Theorem And Proof Youtube According to the mid point theorem, the line joining the mid points of two sides of a triangle is parallel to the third side of the triangle. points \ (c\) and \ (a\) are given on the lines \ (bd\) and \ (be\). study the triangle carefully, then identify and name the parallel lines. Thus, e is the midpoint of ac, which proves the converse of the midpoint theorem. formula. the midpoint formula helps to find the midpoint between the two given points. if m (x 1, y 1) and n (x 2, y 2) are the coordinates of the two given endpoints of a line segment, then the mid point (x, y) formula will be given by. The midpoint theorem tells us that the line segment joining two sides of any triangle at their midpoints is parallel to the third side, and the line segment is half the length of that third side. this at first sounds like nothing but brave talk, so let's test it. the theorem has two assertions. the first is that, for any triangle, connecting. The example is given below to understand the midpoint theorem. example: in triangle abc, the midpoints of bc, ca, and ab are d, e, and f, respectively. find the value of ef, if the value of bc = 14 cm. solution: given: bc = 14 cm. if f is the midpoint of ab and e is the midpoint of ac, then using the midpoint theorem:.

Midpoint Theorem And Converse Euclidean Explained Grade 10 12 Mathdou The midpoint theorem tells us that the line segment joining two sides of any triangle at their midpoints is parallel to the third side, and the line segment is half the length of that third side. this at first sounds like nothing but brave talk, so let's test it. the theorem has two assertions. the first is that, for any triangle, connecting. The example is given below to understand the midpoint theorem. example: in triangle abc, the midpoints of bc, ca, and ab are d, e, and f, respectively. find the value of ef, if the value of bc = 14 cm. solution: given: bc = 14 cm. if f is the midpoint of ab and e is the midpoint of ac, then using the midpoint theorem:. The midpoint theorem can be understood as a triangle with a similarity ratio of 1:2. by connecting the midpoints of a triangle, we can create a similar triangle, and the similarity ratio is 1:2. since they are the midpoints of the sides, it is easy to understand that the similarity ratio is 1:2. Therefore, by converse of mid point theorem e is the mid point of df (fe = de) so, de:ef = 1:1 (as they are equal) example 2: in the figure given below l, m and n are mid points of side pq, qr, and pr respectively of triangle pqr. if pq = 8cm, qr = 9cm and pr = 6cm. find the perimeter of the triangle formed by joining l, m, and n. solution:.

Ignite your personal growth and unlock your true potential as we delve into the realms of self-discovery and self-improvement. Empowering stories, practical strategies, and transformative insights await you on this remarkable path of self-transformation in our Grade 10 Proof For Midpoint Theorem Converse section.

grade 10 proof for midpoint theorem converse

grade 10 proof for midpoint theorem converse Euclidean Geometry Grade 10: Midpoint Theorem Introduction Midpoint theorem and converse Euclidean explained Grade 10+12 (mathdou) Converse of Mid Point Theorem| If a line is drawn through the mid point of one side of a triangle... Midpoint Theorem: Euclidean Geometry Midpoint Theorem | Quadrilaterals | Geometry | Math | LetsTute Geometry I: Similarity, Congruency and the Midpoint Theorem Grade 10-11-12 Midpoint Theorem & Converse Proof | Euclidean Geometry | BATACTION SESSION 4 Example problems (10th mathematics- Triangles) Euclidean Geometry Grade 10: Midpoint Theorem Practice Grade 10: Euclidean Geometry : Midpoint theorem (Examinable) Proof of Converse Mid point Theorem Converse of Mid-Point Theorem -Proof Mathematics | Grade 10 | Midpoint theorem Introduction Grade 10: Converse Midpoint Theorem and Midpoint theorem examples Introduction to Midpoint Theorem- Grade 10 Euclidean Geometry Converse of Mid-point theorem and Proof Grade 12: Euclidean Geometry : Theorem midpoint Grade 10 Euclidean Geometry Exam Questions Part 1

Conclusion

After exploring the topic in depth, one can conclude that this particular content supplies beneficial facts regarding Grade 10 Proof For Midpoint Theorem Converse. Across the whole article, the commentator reveals remarkable understanding on the subject. Markedly, the analysis of X stands out as a highlight. On top of that, the post does a great job in deconstructing complex concepts in an simple manner. On top of that, the essayist offers practical examples that enhance the learning experience. An extra component that differentiates this write-up is the extensive analysis of various aspects related to Grade 10 Proof For Midpoint Theorem Converse. The bloggers scrupulous manner warrants that followers achieve a thorough comprehension of the subject matter. Thanks for spending time on this document. For more details, you are welcome to touch base through the comments. I anticipate your thoughts. In closing, to delve deeper, noted below are a handful of pertinent entries that are useful:Hope you find them interesting!