Hamilton Equations Of Motion Simple Pendulum Constrained To A Parabola

Hamilton Equations Of Motion Simple Pendulum Constrained To A Parabola C constraint equations, and, as we’ll see, n c lagrange multipliers. we will end up with n dof = 3m n c equations of motion. it will thus be more complicated, but we will be able to address the two concerns above. examples we’ll illustrate the following ideas with four examples: the simple pendulum in 2 dimensions. here, the constraint p. The hamiltonian of a pendulum constrained to move on a parabola is a mathematical function that describes the energy of the system, taking into account both the kinetic and potential energy. it is given by the equation h = t v, where t represents the kinetic energy and v represents the potential energy. 2.

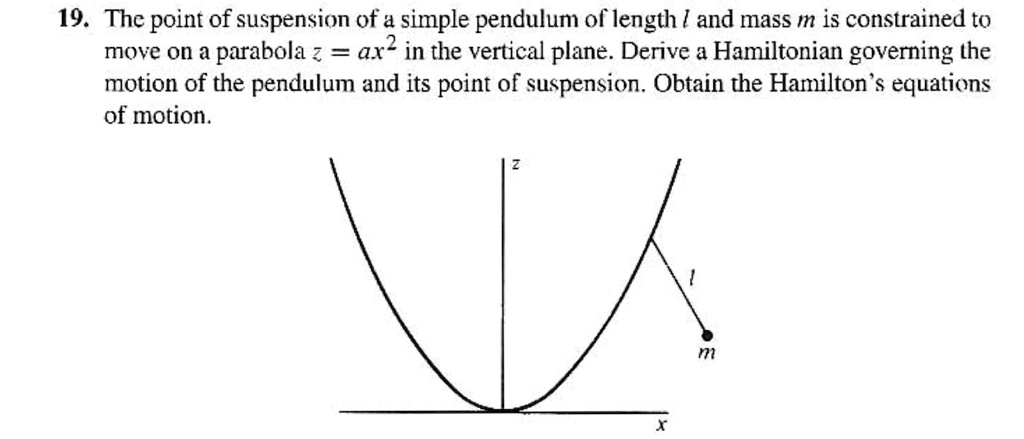
Solved 19 The Point Of Suspension Of A Simple Pendulum Of Length L 1. so you have that the kinetic energy is given by. k = 1 2m(x˙2 y˙2) k = 1 2 m (x ˙ 2 y ˙ 2) if you consider the angle the pendulum makes with the vertical to be θ θ and the length of the pendulum to be l l then you can write. xm =xs lsinθ x m = x s l s i n θ. and. ym =ys − lcosθ y m = y s − l c o s θ. Consider a simple pendulum. the configuration space is clearly a circle, s1,parame terised by an angle 2 [ 1⇡,⇡). the phase space of the pendulum is a cylinder r⇥s , with the r factor corresponding to the momentum. we draw this by flattening out the cylinder. the two di↵erent types of motion are clearly visible in the phase space flows. The hamiltonian h now lets derive another set of equations of motion from the hamiltonian h. this is usually obtained from the system’s lagrangian: begin by de ning the generalized momentum pj @l @q j the lagrange eqn. is then @l @qj = d dt @l @q j = p j example: 1d motion of a single particle: l = 1 2 mq 2 u(q) p = @l @q = mq. H = p2 2mr2 mgr(1 − cos θ) h = p 2 2 m r 2 m g r (1 − cos. ⁡. θ) now hamilton's equations will be: p˙ = −mgr sin θ p ˙ = − m g r sin θ. θ˙ = p mr2 θ ˙ = p m r 2. i know one of the points of hamiltonian formalism is to get first order diff. equations instead of second order that lagrangian formalism gives you, but how can.

Equation Of Motion Of Simple Pendulum Using Hamilton S Equation Of The hamiltonian h now lets derive another set of equations of motion from the hamiltonian h. this is usually obtained from the system’s lagrangian: begin by de ning the generalized momentum pj @l @q j the lagrange eqn. is then @l @qj = d dt @l @q j = p j example: 1d motion of a single particle: l = 1 2 mq 2 u(q) p = @l @q = mq. H = p2 2mr2 mgr(1 − cos θ) h = p 2 2 m r 2 m g r (1 − cos. ⁡. θ) now hamilton's equations will be: p˙ = −mgr sin θ p ˙ = − m g r sin θ. θ˙ = p mr2 θ ˙ = p m r 2. i know one of the points of hamiltonian formalism is to get first order diff. equations instead of second order that lagrangian formalism gives you, but how can. Equations that take the place of newton’s laws and the euler lagrange equations. in section 15.3 we’ll discuss the legendre transform, which is what connects the hamiltonian to the lagrangian. in section 15.4 we’ll give three more derivations of hamilton’s equations, just for the fun of it. finally, in section 15.5 we’ll introduce. University of victoria. in classical mechanics we can describe the state of a system by specifying its lagrangian as a function of the coordinates and their time rates of change: l = l(qi,q˙) (14.3.1) if the coordinates and the velocities increase, the corresponding increment in the lagrangian is. dl = ∑i ∂l ∂qi dqi ∑i ∂l ∂qi.