Hamiltonian For Simple Pendulum And Its Equations Of Motion

Equation Of Motion Of Simple Pendulum Using Hamilton S Equation Of Consider a simple pendulum. the configuration space is clearly a circle, s1,parame terised by an angle 2 [ 1⇡,⇡). the phase space of the pendulum is a cylinder r⇥s , with the r factor corresponding to the momentum. we draw this by flattening out the cylinder. the two di↵erent types of motion are clearly visible in the phase space flows. Hamiltonian for simple pendulum and its equations of motionderive hamiltons equations of motion for a simple pendulumfind the hamiltonian for simple pendulum.

Hamiltonian For Simple Pendulum And Derivation Of Equation Of Motion University of victoria. in classical mechanics we can describe the state of a system by specifying its lagrangian as a function of the coordinates and their time rates of change: l = l(qi,q˙) (14.3.1) if the coordinates and the velocities increase, the corresponding increment in the lagrangian is. dl = ∑i ∂l ∂qi dqi ∑i ∂l ∂qi. The equations of motion in hamiltonian form (6.3), q k= @h @p k q;t; p k= − @h @q k p;t; are almost symmetric in their treatment of q and p. if we de ne a 2n dimensional coordinate for phase space, i = q i n i = p i ˙ for 1 i n; we can write hamilton’s equation in terms of a particular matrix j, j = x2n k=1 j jk @h @ k; where j= 01i n. A simple interpretation of hamiltonian mechanics comes from its application on a one dimensional system consisting of one nonrelativistic particle of mass m. the value h ( p , q ) {\displaystyle h(p,q)} of the hamiltonian is the total energy of the system, in this case the sum of kinetic and potential energy , traditionally denoted t and v. Equations that take the place of newton’s laws and the euler lagrange equations. in section 15.3 we’ll discuss the legendre transform, which is what connects the hamiltonian to the lagrangian. in section 15.4 we’ll give three more derivations of hamilton’s equations, just for the fun of it. finally, in section 15.5 we’ll introduce.

Hamiltonian For Simple Pendulum And Its Equations Of Motion Youtube A simple interpretation of hamiltonian mechanics comes from its application on a one dimensional system consisting of one nonrelativistic particle of mass m. the value h ( p , q ) {\displaystyle h(p,q)} of the hamiltonian is the total energy of the system, in this case the sum of kinetic and potential energy , traditionally denoted t and v. Equations that take the place of newton’s laws and the euler lagrange equations. in section 15.3 we’ll discuss the legendre transform, which is what connects the hamiltonian to the lagrangian. in section 15.4 we’ll give three more derivations of hamilton’s equations, just for the fun of it. finally, in section 15.5 we’ll introduce. A pendulum is a rigid body suspended from a fixed point (hinge) which is offset with respect to the body’s center of mass. if all the mass is assumed to be concentrated at a point, we obtain the idealized simple pendulum. pendulums have played an important role in the history of dynamics. galileo identified the pendulum as the first example. Expression for the hamiltonian as a function of the generalized coordinates and momenta. example use the hamiltonian method to find the equations of motion for a spherical pendulum of mass m and length b. solution. the generalized coordinates are ! and ". the kinetic energy is therefore figure 5.1 – a spherical pendulum with generalized.

Ppt Simple Pendulum Powerpoint Presentation Free Download Id 814485 A pendulum is a rigid body suspended from a fixed point (hinge) which is offset with respect to the body’s center of mass. if all the mass is assumed to be concentrated at a point, we obtain the idealized simple pendulum. pendulums have played an important role in the history of dynamics. galileo identified the pendulum as the first example. Expression for the hamiltonian as a function of the generalized coordinates and momenta. example use the hamiltonian method to find the equations of motion for a spherical pendulum of mass m and length b. solution. the generalized coordinates are ! and ". the kinetic energy is therefore figure 5.1 – a spherical pendulum with generalized.
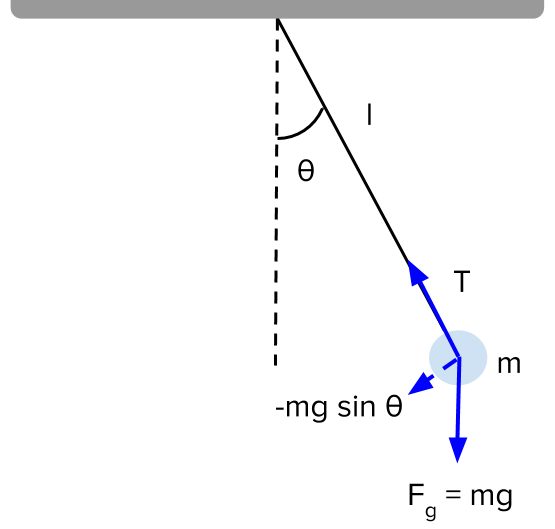
Hamiltonian On Simple Pendulum Motion

Comments are closed.