Hamiltonian On Simple Pendulum Motion

Hamiltonian For Simple Pendulum And Derivation Of Equation Of Motion Consider a simple pendulum. the configuration space is clearly a circle, s1,parame terised by an angle 2 [ 1⇡,⇡). the phase space of the pendulum is a cylinder r⇥s , with the r factor corresponding to the momentum. we draw this by flattening out the cylinder. the two di↵erent types of motion are clearly visible in the phase space flows. Hamiltonian for simple pendulum and its equations of motionderive hamiltons equations of motion for a simple pendulumfind the hamiltonian for simple pendulum.

Hamiltonian For Simple Pendulum And Its Equations Of Motion Youtube University of victoria. in classical mechanics we can describe the state of a system by specifying its lagrangian as a function of the coordinates and their time rates of change: l = l(qi,q˙) (14.3.1) if the coordinates and the velocities increase, the corresponding increment in the lagrangian is. dl = ∑i ∂l ∂qi dqi ∑i ∂l ∂qi. H = p2 2mr2 mgr(1 − cos θ) h = p 2 2 m r 2 m g r (1 − cos. ⁡. θ) now hamilton's equations will be: p˙ = −mgr sin θ p ˙ = − m g r sin θ. θ˙ = p mr2 θ ˙ = p m r 2. i know one of the points of hamiltonian formalism is to get first order diff. equations instead of second order that lagrangian formalism gives you, but how can. A pendulum is a rigid body suspended from a fixed point (hinge) which is offset with respect to the body’s center of mass. if all the mass is assumed to be concentrated at a point, we obtain the idealized simple pendulum. pendulums have played an important role in the history of dynamics. galileo identified the pendulum as the first example. A simple interpretation of hamiltonian mechanics comes from its application on a one dimensional system consisting of one nonrelativistic particle of mass m. the value h ( p , q ) {\displaystyle h(p,q)} of the hamiltonian is the total energy of the system, in this case the sum of kinetic and potential energy , traditionally denoted t and v.

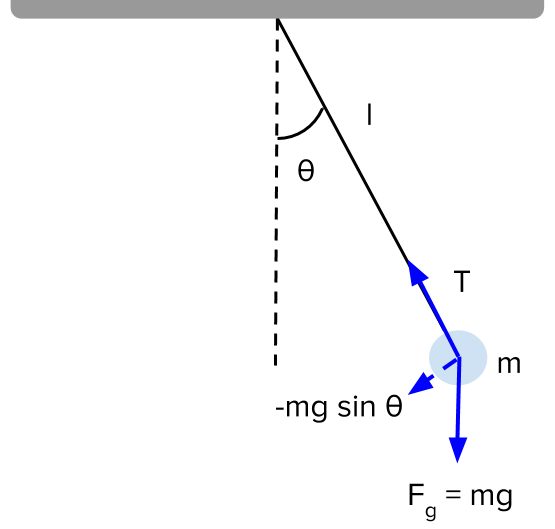
Hamiltonian On Simple Pendulum Motion A pendulum is a rigid body suspended from a fixed point (hinge) which is offset with respect to the body’s center of mass. if all the mass is assumed to be concentrated at a point, we obtain the idealized simple pendulum. pendulums have played an important role in the history of dynamics. galileo identified the pendulum as the first example. A simple interpretation of hamiltonian mechanics comes from its application on a one dimensional system consisting of one nonrelativistic particle of mass m. the value h ( p , q ) {\displaystyle h(p,q)} of the hamiltonian is the total energy of the system, in this case the sum of kinetic and potential energy , traditionally denoted t and v. A simple pendulum motion is an object of mass m hanging on a string from a pivot point so that it is constrained to move on a circle of a fixed radius. if we map the space in cartesian coordinates, the simple pendulum motion is a 2 dimensional problem, both the position, r, and the speed, v, have 2 components:. The equations of motion of a system can be derived using the hamiltonian coupled with hamilton’s equations of motion, that is, equations \((8.3.11 8.3.13)\). formally the hamiltonian is constructed from the lagrangian. that is. select a set of independent generalized coordinates \(q {i}\) partition the active forces.

Equation Of Motion Of Simple Pendulum Using Hamilton S Equation Of A simple pendulum motion is an object of mass m hanging on a string from a pivot point so that it is constrained to move on a circle of a fixed radius. if we map the space in cartesian coordinates, the simple pendulum motion is a 2 dimensional problem, both the position, r, and the speed, v, have 2 components:. The equations of motion of a system can be derived using the hamiltonian coupled with hamilton’s equations of motion, that is, equations \((8.3.11 8.3.13)\). formally the hamiltonian is constructed from the lagrangian. that is. select a set of independent generalized coordinates \(q {i}\) partition the active forces.