How To Draw Reference Angle

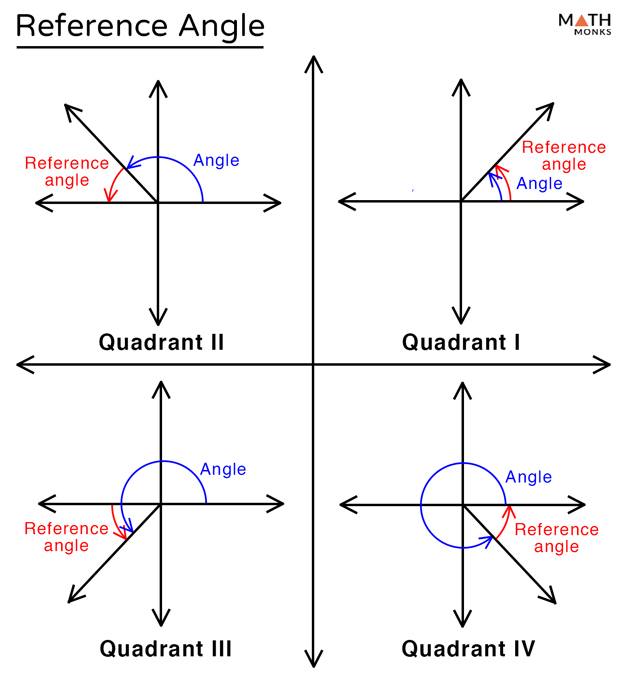
Reference Angle Definition And Formulas With Examples A reference angle is always positive irrespective of which side of the axis it is falling. how to draw reference angle? to draw the reference angle for an angle, identify its terminal side and see by what angle the terminal side is close to the x axis. the reference angle of 135° is drawn below: here, 45° is the reference angle of 135°. 90° to 180°: reference angle = 180° − angle, 180° to 270°: reference angle = angle − 180°, 270° to 360°: reference angle = 360° − angle. in this case, we need to choose the formula reference angle = angle − 180°. substitute your angle into the equation to find the reference angle: reference angle = 250° − 180° = 70°.

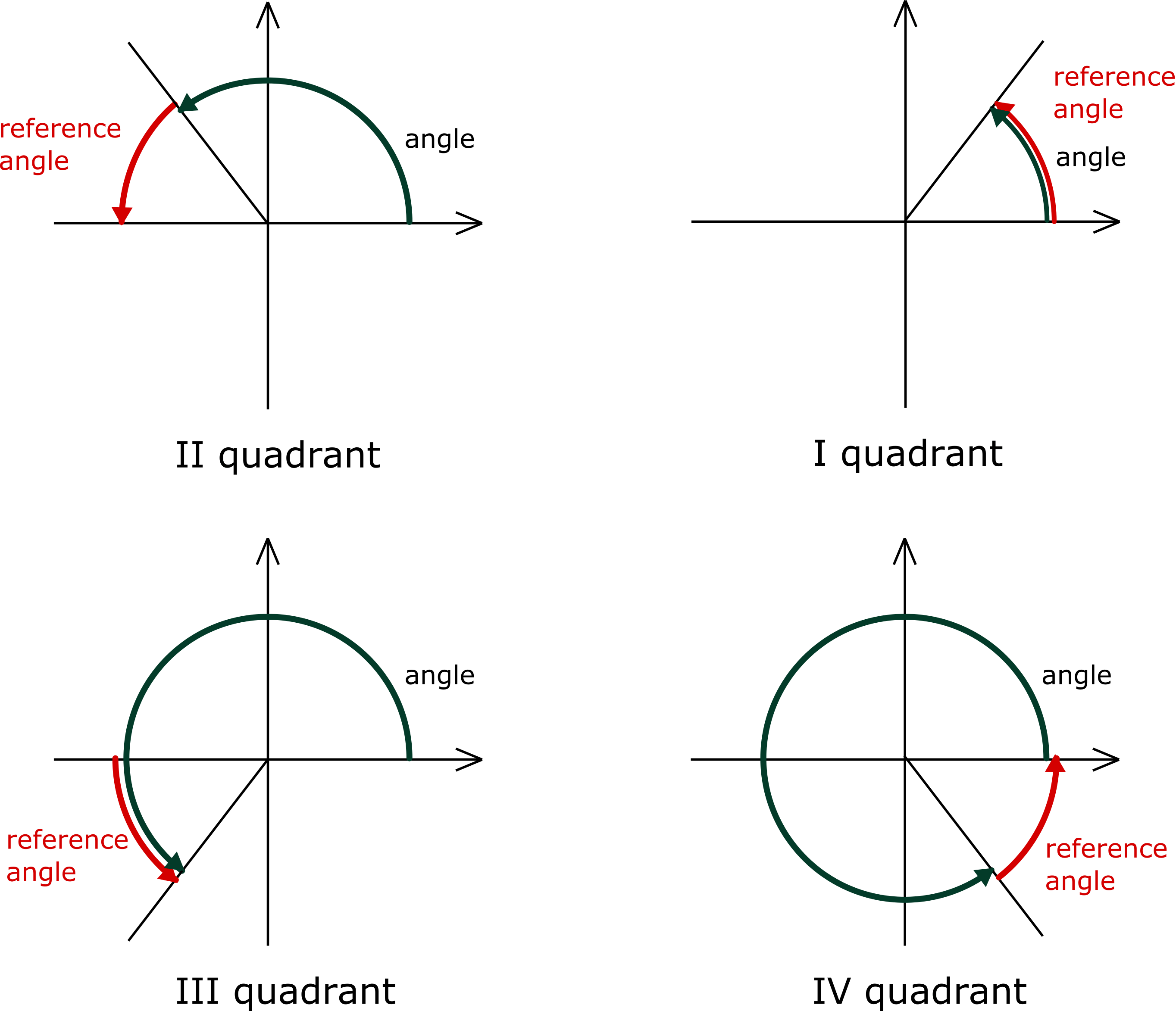
Reference Angle Calculator Definition Graph Quadrants Find reference angle. the reference angle is the positive acute angle that can represent an angle of any measure. the reference angle must be <90∘ must be <90 ∘. in radian measure, the reference angle must be <π 2 must be <π 2. basically, any angle on the x y plane has a reference angle, which is always between 0 and 90 degrees. When the angle given to you is in the fourth quadrant, subtract the angle from 360° to get the reference angle, or . if the angle is in radians, subtract the angle from 2𝛑, or . [7] for example, find the reference angle. θ 1 {\displaystyle {\theta }^ {1}} if your given angle is. θ {\displaystyle {\theta }} = 325°. 150° is located in the second quadrant. the angle it makes with the x axis is 180° − 150° = 30°, so the reference angle is 30°.this tells us that 150° has the same sine and cosine values as 30°, except for the sign. we know that. cos (3 0 ∘) = 3 2 a n d sin (3 0 ∘) = 1 2. How to use reference angles to find the sine, cosine and tangent of non acute angles? to find the value of sine, cosine and tangent at non acute angles (from 90 to 360), first draw the angle on the unit circle and find the reference angle. a reference angle is formed by the terminal side and the x axis and will therefore always be acute.

5 3 Finding Reference Angles And Drawing Reference Triangles Youtube 150° is located in the second quadrant. the angle it makes with the x axis is 180° − 150° = 30°, so the reference angle is 30°.this tells us that 150° has the same sine and cosine values as 30°, except for the sign. we know that. cos (3 0 ∘) = 3 2 a n d sin (3 0 ∘) = 1 2. How to use reference angles to find the sine, cosine and tangent of non acute angles? to find the value of sine, cosine and tangent at non acute angles (from 90 to 360), first draw the angle on the unit circle and find the reference angle. a reference angle is formed by the terminal side and the x axis and will therefore always be acute. Reference angle = 360° – given angle. 2) when calculated in radians. when calculated in radians: 180° = π, 360° = 2π, 270 = 2π 2, and 90° = π 2. thus, the formulas become: case 1: (for angles between 0° to 90°) – first quadrant. reference angle = given angle. case 2: (for angles between 90° to 180°) – second quadrant. A reference angle, denoted θ^ θ ^, is the positive acute angle between the terminal side of θ θ and the x x axis. the word reference is used because all angles can refer to qi. that is, memorization of ordered pairs is confined to qi of the unit circle. if a standard angle θ θ has a reference angle of 30˚ 30 ˚, 45˚ 45 ˚, or 60˚ 60.

Reference Angle Explanation Formula And Examples Education Spike Reference angle = 360° – given angle. 2) when calculated in radians. when calculated in radians: 180° = π, 360° = 2π, 270 = 2π 2, and 90° = π 2. thus, the formulas become: case 1: (for angles between 0° to 90°) – first quadrant. reference angle = given angle. case 2: (for angles between 90° to 180°) – second quadrant. A reference angle, denoted θ^ θ ^, is the positive acute angle between the terminal side of θ θ and the x x axis. the word reference is used because all angles can refer to qi. that is, memorization of ordered pairs is confined to qi of the unit circle. if a standard angle θ θ has a reference angle of 30˚ 30 ˚, 45˚ 45 ˚, or 60˚ 60.

Angle Reference Drawing

Easy Way To Draw Types Of Angles Drawing For Students School