How To Draw Reference Frames For Two Moving Object
Frame Of Reference Bartleby We can extend equation 4.6.3 to any number of reference frames. for particle p with velocities →vpa, →vpb, and →vpc in frames a, b, and c, →vpc = →vpa →vab →vbc. we can also see how the accelerations are related as observed in two reference frames by differentiating equation 4.6.3: →aps = →aps →as s. So it is just a simple frame change: let the earth frame be frame e and the frame moving with object 1 be frame 1, then the velocity we want is v12 (“velocity of object 2 in frame 1”). if we make the change a → 1, b → e, and p → 2 in equation (1.3.7), we get. v12 = ve2 − ve1. in other words, the velocity of 2 relative to 1 is just.

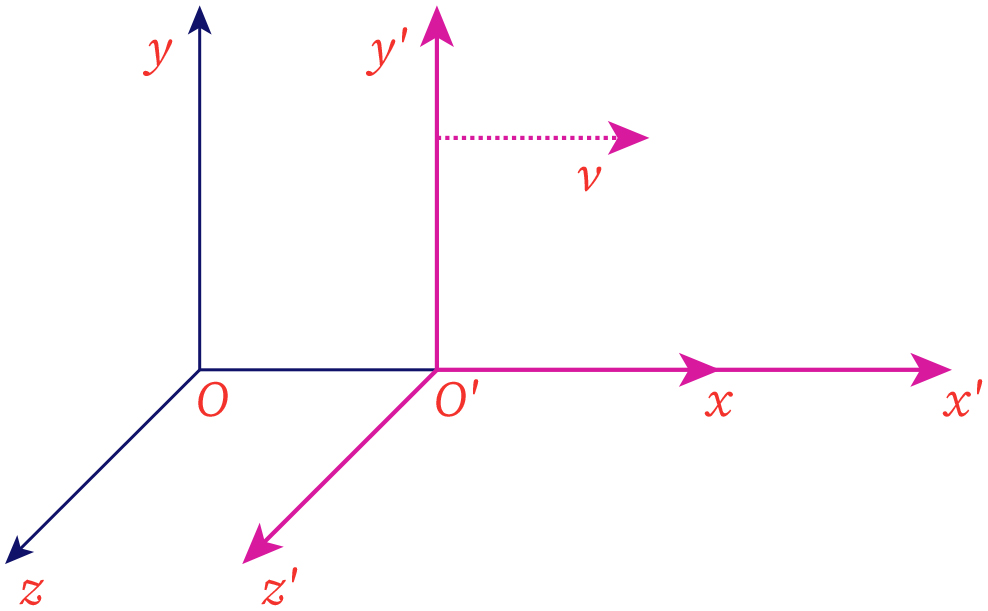
Reference Frames Youtube Draw the position and velocity vectors for relative motion. analyze one dimensional and two dimensional relative motion problems using the position and velocity vector equations. motion does not happen in isolation. if you’re riding in a train moving at 10 m s east, this velocity is measured relative to the ground on which you’re traveling. Draw the position and velocity vectors for relative motion. analyze one dimensional and two dimensional relative motion problems using the position and velocity vector equations. motion does not happen in isolation. if you’re riding in a train moving at 10 m s east, this velocity is measured relative to the ground on which you’re traveling. Let's see if we can put the above example into this language. there are three entities here. two are frames and on is a moving object. the moving object is ann, and she is being observed by bob, in the reference frame of the train, and chu, in the reference frame of the earth. in the example, we expressed three different relative velocity vectors:. The radius of the circle of revolution at latitude λ is recosλ. the velocity of the body is 2πr t. ac = 4π2recosλ t2 for λ = 40°, ac = 0.26%g. a proton in a synchrotron is moving in a circle of radius 1 km and increasing its speed by v(t) = c1 c2t2, wherec1 = 2.0 × 105m s, c2 = 105m s3.

Isaac Physics Let's see if we can put the above example into this language. there are three entities here. two are frames and on is a moving object. the moving object is ann, and she is being observed by bob, in the reference frame of the train, and chu, in the reference frame of the earth. in the example, we expressed three different relative velocity vectors:. The radius of the circle of revolution at latitude λ is recosλ. the velocity of the body is 2πr t. ac = 4π2recosλ t2 for λ = 40°, ac = 0.26%g. a proton in a synchrotron is moving in a circle of radius 1 km and increasing its speed by v(t) = c1 c2t2, wherec1 = 2.0 × 105m s, c2 = 105m s3. Figure 1: path of the ball as seen by an observer on the train and an observer at the station. the different observations occur because the two observers are in different frames of reference. a frame of reference is a set of coordinates that can be used to determine positions and velocities of objects in that frame; different frames of. Strategy. first, we must establish the reference frame common to both vehicles, which is earth. then, we write the velocities of each with respect to the reference frame of earth, which enables us to form a vector equation that links the car, the truck, and earth to solve for the velocity of the car with respect to the truck.

Frame Of Reference Space And Time Inertial And Non Inertial Frames Figure 1: path of the ball as seen by an observer on the train and an observer at the station. the different observations occur because the two observers are in different frames of reference. a frame of reference is a set of coordinates that can be used to determine positions and velocities of objects in that frame; different frames of. Strategy. first, we must establish the reference frame common to both vehicles, which is earth. then, we write the velocities of each with respect to the reference frame of earth, which enables us to form a vector equation that links the car, the truck, and earth to solve for the velocity of the car with respect to the truck.

Comments are closed.