How To Draw Reference Triangles
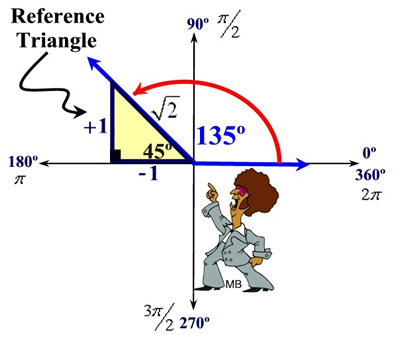
Reference Triangles Mathbitsnotebook A2 Example 1: find the exact value of sin 135º. (see diagram above) solution: draw the angle in standard position (with initial ray on the x axis and opening counterclockwise). find the reference angle (in this case 45º). draw the reference triangle. label the sides of the triangle with the patterns for a 45º 45º 90º triangle, being careful. How to determine the reference angle for any angle in degrees or radians. i also show you how to draw the reference triangles. see note below!note: at 6:39,.

5 3 Finding Reference Angles And Drawing Reference Triangles Youtube Now then, a reference triangle is a right triangle formed when you construct (drop) a perpendicular from the terminal side of an angle in standard position to the x axis. these triangles will form a shape that is similar to a x wing fighter or a bowtie, as indicated by math bits notebook, and allow us to find distances (lengths). A brief introduction to reference triangles. this video also talks about how to evaluate trig functions of angles associated with points that are not on the. Activity: reference angles. use a protractor to draw an angle of \(56^{\circ}\) in standard position. draw its reference triangle. use your calculator to find the sine and cosine of \(56^{\circ}\), rounded to two decimal places. label the sides of the reference triangle with their lengths. Using reference angles to evaluate trigonometric functions. we can find the cosine and sine of any angle in any quadrant if we know the cosine or sine of its reference angle. the absolute values of the cosine and sine of an angle are the same as those of the reference angle. the sign depends on the quadrant of the original angle.
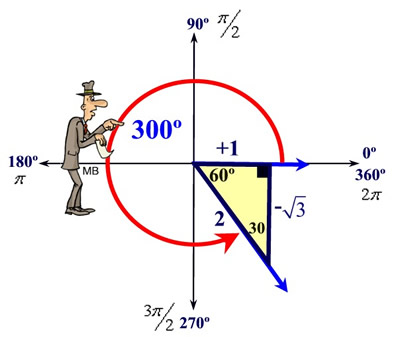
Reference Triangles Mathbitsnotebook A2 Ccss Math Activity: reference angles. use a protractor to draw an angle of \(56^{\circ}\) in standard position. draw its reference triangle. use your calculator to find the sine and cosine of \(56^{\circ}\), rounded to two decimal places. label the sides of the reference triangle with their lengths. Using reference angles to evaluate trigonometric functions. we can find the cosine and sine of any angle in any quadrant if we know the cosine or sine of its reference angle. the absolute values of the cosine and sine of an angle are the same as those of the reference angle. the sign depends on the quadrant of the original angle. To find (or recall) the trig values for 30° and 60° angles: draw an equilateral triangle having sides of length 2. drop the altitude line from the peak to the midpoint of the base, forming two smaller triangles. relabel the base as now have two lengths of 1. label the various angles and the altitude with their values. A reference triangle is a triangle relative to which trilinear coordinates, exact trilinear coordinates, derived triangle, or other objects are defined in triangle geometry (kimberling 1998, p. 155). for example, in the construction "take a triangle deltaabc, its excentral triangle, then its tangential triangle," deltaabc is the reference triangle." for example, the orthic triangle is.

Comments are closed.