Solved A Square Is Inscribed In An Equilateral Triangle As Shown Find H = a × √3 2. substituting h into the first area formula, we obtain the equation for the equilateral triangle area: area = a² × √3 4. 2. using trigonometry. let's start with the trigonometric triangle area formula: area = (1 2) × a × b × sin(γ), where γ is the angle between the sides. we remember that all sides and all angles. It means we can easily find the side length by dividing the perimeter by. we found the side of the equilateral triangle to be inches. upon knowing the measure of one of its side, we should now be able to find its area using the formula. example 4: the area of an equilateral triangle is 10 square centimeters.
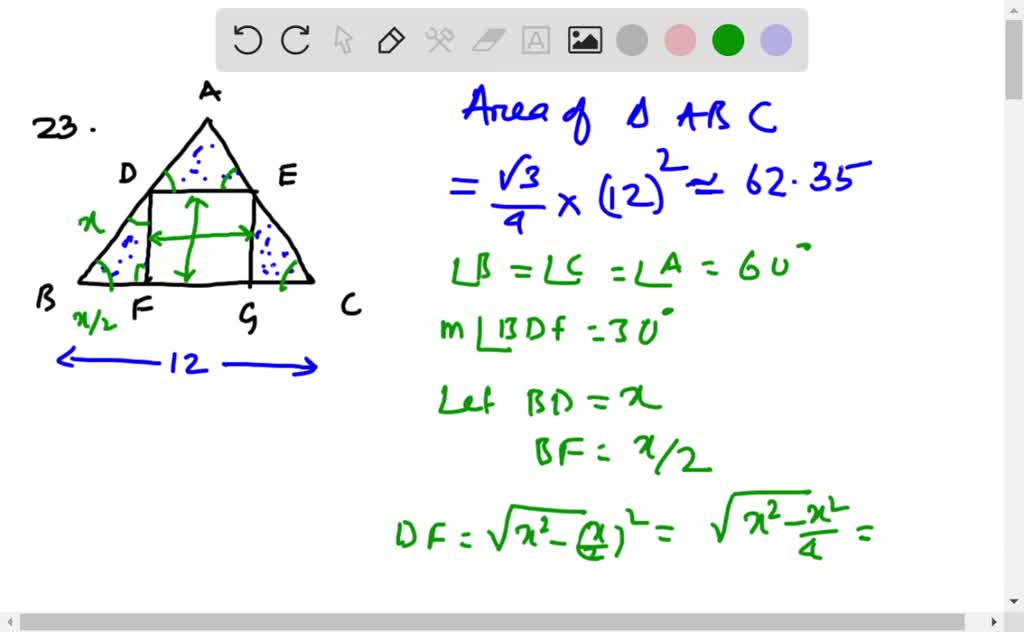
Area Of An Equilateral Triangle Formula Examples Definition $\begingroup$ @handebruijn because if you choose any square inside the triangle that does not fit the definition that i gave, an equilateral triangle of smallest area which covers this square will have less area than the first equilateral triangle. in the other words, try to draw an equiateral triangle of smallest area which covers a square. Examples on area of equilateral triangle. example 1: find the area of an equilateral triangle of side 9 cm. solution: the formula for the area of an equilateral triangle is given as, area = √ (3) 4 × (side) 2. by substituting the value of side length in the above formula, we get, = √ (3) 4 × 9 2. = 35.07 inches 2. The story of why we know that the largest equilateral triangle inscribed in a square is positioned as shown below, can be found in a video here. just press the green button marked "video". just press the green button marked "video". Let the side of the equilateral triangle be s = ae = ef = af. triangles abe and afd are congruent. this is because they are both right triangles whose hypotenuse is s and longer leg is 1. by the gougu theorem (aka pythagorean theorem), the remaining leg in each triangle has length described by: df = be = x s 2 = 1 2 x 2 s 2 = 1 x 2. we then.
How To Find The Area Of An Equilateral Triangle Inscribed In A Square The story of why we know that the largest equilateral triangle inscribed in a square is positioned as shown below, can be found in a video here. just press the green button marked "video". just press the green button marked "video". Let the side of the equilateral triangle be s = ae = ef = af. triangles abe and afd are congruent. this is because they are both right triangles whose hypotenuse is s and longer leg is 1. by the gougu theorem (aka pythagorean theorem), the remaining leg in each triangle has length described by: df = be = x s 2 = 1 2 x 2 s 2 = 1 x 2. we then. If you know the lengths of all sides (a, b, and c) of a triangle, you can compute its area: calculate half of the perimeter ½(a b c). denote this value by s. compute s a, s b, and s c. multiply the three numbers from step 2. multiply the result by s. take the square root of the result. Formulas and calculations for a equilateral triangle: perimeter of equilateral triangle: p = 3a. semiperimeter of equilateral triangle: s = 3a 2. area of equilateral triangle: k = (1 4) * √3 * a 2. altitude of equilateral triangle h = (1 2) * √3 * a. angles of equilateral triangle: a = b = c = 60°.
Comments are closed.