How To Find Trigonometric Ratios Given A Right Triangle Trigonometry
How To Find Trigonometric Ratios Given A Right Triangle Trigonometry To solve a right triangle using trigonometry: identify an acute angle in the triangle α. for this angle: sin(α) = opposite hypotenuse; and. cos(α) = adjacent hypotenuse. by taking the inverse trigonometric functions, we can find the value of the angle α. you can repeat the procedure for the other angle. Trigonometry calculator as a tool for solving right triangle. to find the missing sides or angles of the right triangle, all you need to do is enter the known variables into the trigonometry calculator. you need only two given values in the case of: one side and one angle. two sides. area and one side. remember that if you know two angles, it's.

How To Find The Six Trigonometric Ratios Given A Right Triangle Soh To get to this answer: you can use the formula that relates the hypotenuse (c) to any of the legs (a) of a 45 45 90 triangle: c = a × √2. and solve for the leg a: a = c √2 = (10√5 in) √2 = 5√10 in = 15.81 in. trig identities calculator. given side length a. side length b. Using the theorem of pythagoras x2 y2 = r2 and knowing r = 4, x = 1, we obtain 12 y2 = 42. thus, y2 = 16 − 1 = 15 and so y = √15. now that all three sides of the right triangle are known, the definitions can be used to find the other five trigonometric ratios. sinθ = y r = √15 4 cosθ = x r = 1 4 tanθ = y x = √15. Right triangle trigonometry trigonometric ratios example find the sine, cosine, and tangent ratios for each of the acute angles in the following triangle. solution: we first find the missing length of side rs. solving the equation ( ) 12 13rs 22 2 =, we obtain rs =5. we then find the three basic trigonometric ratios for angle r:. Three functions, but same idea. right triangle. sine, cosine and tangent are the main functions used in trigonometry and are based on a right angled triangle before getting stuck into the functions, it helps to give a name to each side of a right triangle:.

Right Triangle Trigonometry Finding The Six Trigonometric Ratios Youtube Right triangle trigonometry trigonometric ratios example find the sine, cosine, and tangent ratios for each of the acute angles in the following triangle. solution: we first find the missing length of side rs. solving the equation ( ) 12 13rs 22 2 =, we obtain rs =5. we then find the three basic trigonometric ratios for angle r:. Three functions, but same idea. right triangle. sine, cosine and tangent are the main functions used in trigonometry and are based on a right angled triangle before getting stuck into the functions, it helps to give a name to each side of a right triangle:. If needed, draw the right triangle and label the angle provided. identify the angle, the adjacent side, the side opposite the angle, and the hypotenuse of the right triangle. find the required function: sine as the ratio of the opposite side to the hypotenuse. cosine as the ratio of the adjacent side to the hypotenuse. Step 1: identify the sides of the right triangle and their lengths. based on the location of θ and the right angle in the right triangle, we can determine the names and lengths of each side.
Trigonometrical Ratios Igcse At Mathematics Realm If needed, draw the right triangle and label the angle provided. identify the angle, the adjacent side, the side opposite the angle, and the hypotenuse of the right triangle. find the required function: sine as the ratio of the opposite side to the hypotenuse. cosine as the ratio of the adjacent side to the hypotenuse. Step 1: identify the sides of the right triangle and their lengths. based on the location of θ and the right angle in the right triangle, we can determine the names and lengths of each side.
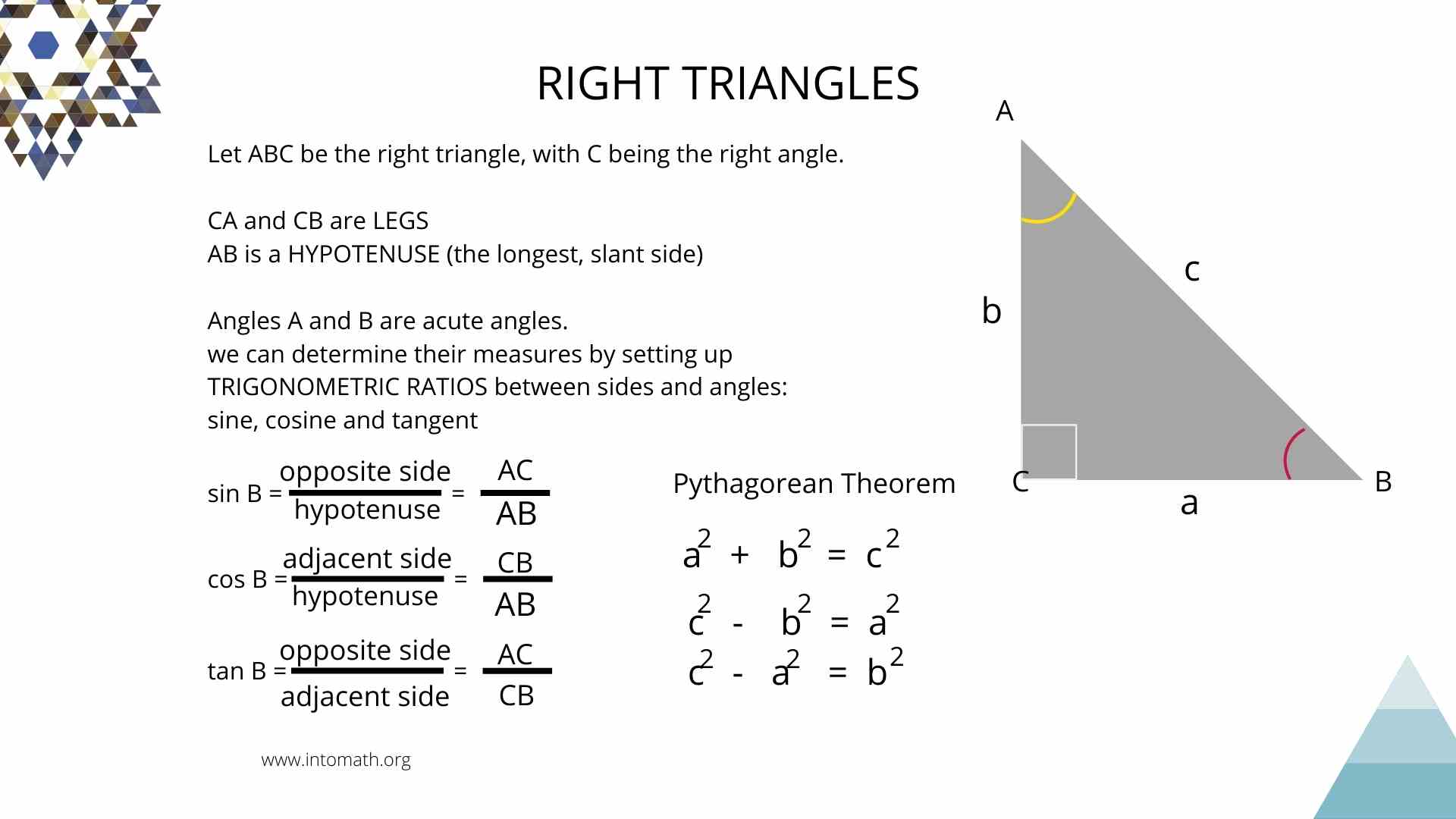
Lesson 5 Right Triangle Trigonometry Trig Ratios Intomath

Comments are closed.