How To Locate The Focal Points Of An Ellipse

Foci Of Ellipse Definition Formula Example Faqs Formula for the focus of an ellipse. diagram 1. the formula generally associated with the focus of an ellipse is c2 =a2 −b2 c 2 = a 2 − b 2 where c c is the distance from the focus to center, a a is the distance from the center to a vetex and b b is the distance from the center to a co vetex . Learn how to find the focus points (foci) of an ellipse given its two axis.this channel is dedicated to teaching people how to improve their technica.

How To Locate The Focal Points Of An Ellipse Youtube 12.5. an ellipse has two focus points. the word foci (pronounced ' foe sigh') is the plural of 'focus'. one focus, two foci. the foci always lie on the major (longest) axis, spaced equally each side of the center. if the major axis and minor axis are the same length, the figure is a circle and both foci are at the center. Finding the foci of an ellipse. remember the two patterns for an ellipse: each ellipse has two foci (plural of focus) as shown in the picture here: as you can see, c is the distance from the center to a focus. we can find the value of c by using the formula c2 = a2 b2. notice that this formula has a negative sign, not a positive sign like the. Example 1: find the coordinates of the foci of ellipse having an equation x 2 25 y 2 16 = 0. solution: the given equation of the ellipse is x 2 25 y 2 16 = 0. commparing this with the standard equation of the ellipse x 2 a 2 y 2 b 2 = 1, we have a = 5, and b = 4. let us first calculate the eccentricity of the ellipse. In conic sections, a conic having its eccentricity less than 1 is called an ellipse. i.e, the locus of points whose distances from a fixed point and straight line are in constant ratio ‘e’ which is less than 1, is called an ellipse. the fixed point and fixed straight line are called focus and directrix respectively. an ellipse has two.
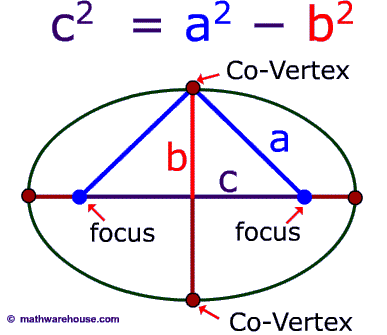
Focus Of Ellipse The Formula For The Focus And Example 1: find the coordinates of the foci of ellipse having an equation x 2 25 y 2 16 = 0. solution: the given equation of the ellipse is x 2 25 y 2 16 = 0. commparing this with the standard equation of the ellipse x 2 a 2 y 2 b 2 = 1, we have a = 5, and b = 4. let us first calculate the eccentricity of the ellipse. In conic sections, a conic having its eccentricity less than 1 is called an ellipse. i.e, the locus of points whose distances from a fixed point and straight line are in constant ratio ‘e’ which is less than 1, is called an ellipse. the fixed point and fixed straight line are called focus and directrix respectively. an ellipse has two. This video explains how to find the foci of an ellipse from its equation. This video shows how to find the focal points, normal, and tangent of an ellipse.

How To Find The Equation Of An Ellipse With Foci And Points This video explains how to find the foci of an ellipse from its equation. This video shows how to find the focal points, normal, and tangent of an ellipse.
Focal Points Of An Ellipse Geogebra

Comments are closed.