How To Set Up Double Integrals

Setting Up A Double Integral Using Both Orders Of Integration Youtube Theorem: double integrals over nonrectangular regions. suppose g(x, y) is the extension to the rectangle r of the function f(x, y) defined on the regions d and r as shown in figure 15.2.1 inside r. then g(x, y) is integrable and we define the double integral of f(x, y) over d by. ∬ d f(x, y)da = ∬ r g(x, y)da. Volume = ∬ r f (x,y) da volume = ∬ r f (x, y) d a. we can use this double sum in the definition to estimate the value of a double integral if we need to. we can do this by choosing (x∗ i,y∗ j) (x i ∗, y j ∗) to be the midpoint of each rectangle. when we do this we usually denote the point as (¯¯xi,¯¯yj) (x ¯ i, y ¯ j).

How To Solve Double Integrals Steps Youtube Double integrals can be used to find the volume under a surface, but how exactly do they work and how do you set one up?~~~this video was funded by texas a&m. The second geometric interpretation of a double integral is the following. area of d = ∬ d da. this is easy to see why this is true in general. let’s suppose that we want to find the area of the region shown below. from calculus i we know that this area can be found by the integral, a = ∫b ag2(x) − g1(x)dx. Example 14.1.1: setting up a double integral and approximating it by double sums. consider the function z = f(x, y) = 3x2 − y over the rectangular region r = [0, 2] × [0, 2] (figure 14.1.4). set up a double integral for finding the value of the signed volume of the solid s that lies above r and “under” the graph of f. The double integral uses two integration symbols to represent a "double sum.''. when adding up the volumes of rectangular solids over a partition of a region , as done in figure , one could first add up the volumes across each row (one type of sum), then add these totals together (another sum), as in.
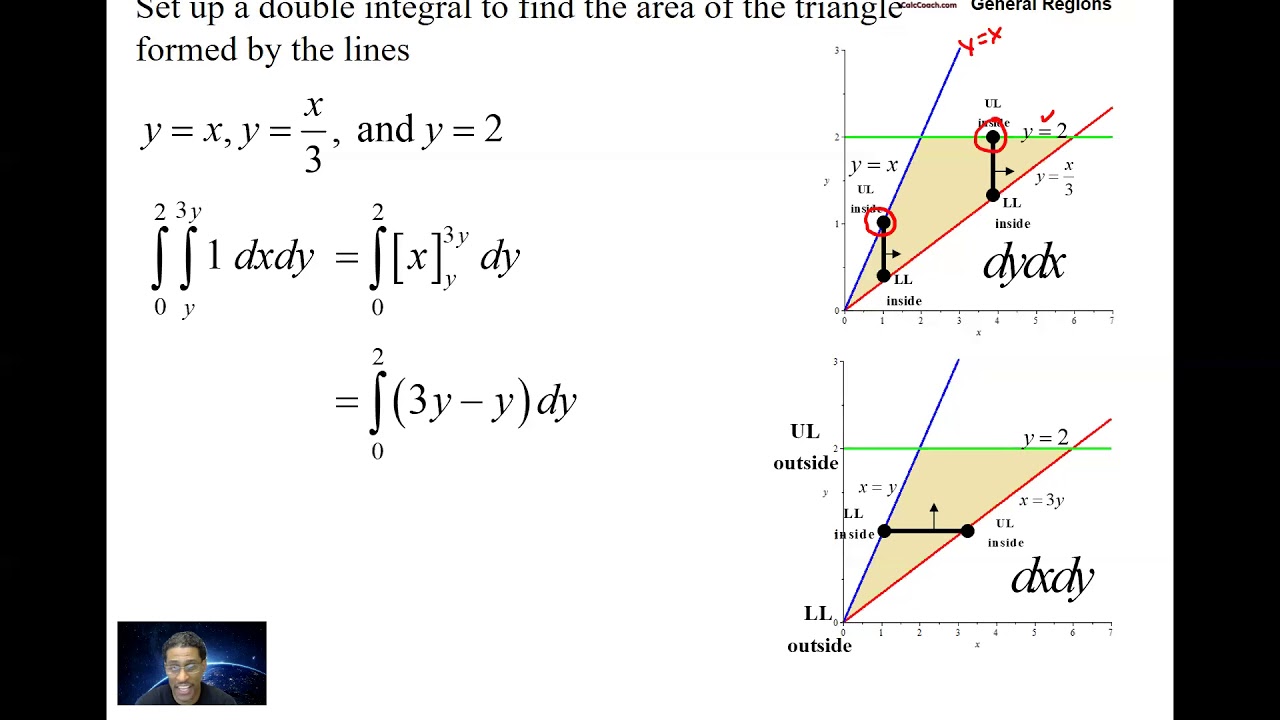
Area As A Double Integral And Setting Up Multiple Double Integrals In Example 14.1.1: setting up a double integral and approximating it by double sums. consider the function z = f(x, y) = 3x2 − y over the rectangular region r = [0, 2] × [0, 2] (figure 14.1.4). set up a double integral for finding the value of the signed volume of the solid s that lies above r and “under” the graph of f. The double integral uses two integration symbols to represent a "double sum.''. when adding up the volumes of rectangular solids over a partition of a region , as done in figure , one could first add up the volumes across each row (one type of sum), then add these totals together (another sum), as in. Set up a double integral in rectangular coordinates for calculating the volume of the solid under the graph of the function \(f(x,y) = 33 x^{2} y^{2}\) and above the plane \(z = 8\text{.}\) instructions: please enter the integrand in the first answer box. Khan academy. if you're seeing this message, it means we're having trouble loading external resources on our website. if you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked. explore. search. donate. log in sign up.

Comments are closed.