If Two Parallel Lines Are Intersected By A Transversal Then Prove That

By viagraultimate On Nov 11, 2024 Last updated

If Two Parallel Lines Are Intersected By A Transversal Then Prove That Ef be the transversal passing through the two parallel lines at p and q respectively. p r and q s are the bisectors of ∠ e p b and ∠ p q d . according to the corresponding angles postulate if a transversal intersects two parallel lines, the corresponding angles will be always equal. Thus, if two parallel lines are intersected by a transversal, then bisectors of the interior angles form a rectangle. note: the sum of interior angles on the same side of the transversal is equal to \[{180^\circ}\]. when two lines are crossed by another line which is called as the transversal the alternate interior angles are equal.

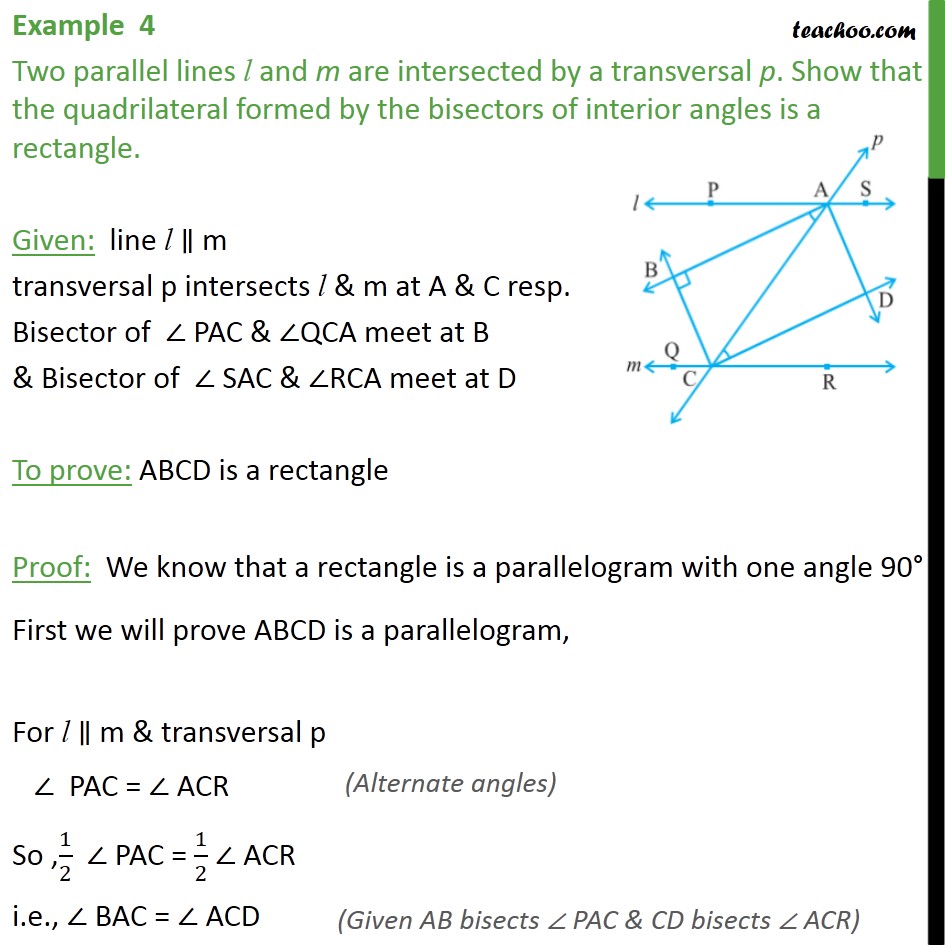
Example 4 Two Parallel Lines L And M Are Intersected Examples The converse of alternate interior angles theorem states that if two lines are intersected by a transversal forming congruent alternate interior angles, then the lines are parallel. thus according to the converse of alternate interior angles theorem, the below given lines will be parallel if ∠d is 40° and ∠b is 140°. Example 1: identify the corresponding angles in the figure which shows two parallel lines 'm' and 'n' cut by a transversal 't'. solution: in the given figure, two parallel lines are cut by a transversal, and the corresponding angles in the figure are ∠1 and ∠3; and ∠2 and ∠5. example 2: find the value of x in the given parallel lines 'a. Given, a transversal intersects two parallel lines. we have to prove that the bisectors of any pair of corresponding angles formed are parallel. consider two parallel lines ab and cd cut by a transversal hg. we know that if a transversal intersects two parallel lines, then corresponding angles are equal and conversely. the corresponding angles. 5. identify: what are the transversals of a b ↔ and b d ↔. solution: the transversals of a b ↔ are a c ↔ and b d ↔. the transversals of b d ↔ are a b ↔ and c d ↔. 6. calculate: given m ∠ 1 = 70 °, determine the measures of all other fifteen angles in this diagram using whatever theorems or postulates you would like.

If Two Parallel Lines Are Intersected By A Transversal Then Prove That Given, a transversal intersects two parallel lines. we have to prove that the bisectors of any pair of corresponding angles formed are parallel. consider two parallel lines ab and cd cut by a transversal hg. we know that if a transversal intersects two parallel lines, then corresponding angles are equal and conversely. the corresponding angles. 5. identify: what are the transversals of a b ↔ and b d ↔. solution: the transversals of a b ↔ are a c ↔ and b d ↔. the transversals of b d ↔ are a b ↔ and c d ↔. 6. calculate: given m ∠ 1 = 70 °, determine the measures of all other fifteen angles in this diagram using whatever theorems or postulates you would like. In the diagram shown on page 330, the two lines cut by the transversal are not parallel lines. however, when two lines are parallel, many statements may be postulated and proved about these angles. theorem 9.1a given and are cut by transversal at points e and f, respectively; 1 2. prove proof to prove this theorem, we will use an indirect proof. If two parallel lines are intersected by a transverse line, then the bisectors of the interior angles forms: q. prove that if two parallel lines are intersected by a transversal, then the bisectors of the interior angles on the same side of the transversal intersect at right angles.

Prove That If Two Parallel Lines Are Intersected By A Transversal Then In the diagram shown on page 330, the two lines cut by the transversal are not parallel lines. however, when two lines are parallel, many statements may be postulated and proved about these angles. theorem 9.1a given and are cut by transversal at points e and f, respectively; 1 2. prove proof to prove this theorem, we will use an indirect proof. If two parallel lines are intersected by a transverse line, then the bisectors of the interior angles forms: q. prove that if two parallel lines are intersected by a transversal, then the bisectors of the interior angles on the same side of the transversal intersect at right angles.

Prepare to be captivated by the magic that If Two Parallel Lines Are Intersected By A Transversal Then Prove That has to offer. Our dedicated staff has curated an experience tailored to your desires, ensuring that your time here is nothing short of extraordinary.

If two parallel lines are intersected by a transversal prove that the bisectors of the two pairs of

If two parallel lines are intersected by a transversal prove that the bisectors of the two pairs of if two parallel lines are intersected by a transversal then prove that the bisector form a rectangle Parallel Lines cut by a Transversal If two parallel lines are intersected by a transversal then prove that bisectors of the two pairs of If two parallel lines are intersected by a transversal, then prove that bisectors of interior angles Proof: Alternate Interior Angles Are Congruent Class 9-Lines & Angles-RD Sharma-Pg10.28 Th5, If two parallel lines are intersected by a transversal When two parallel lines are cut by a transversal, the pair of corresponding angles are always equal. If two parallel lines are intersected by a transversal, prove that the bisectors of the two pairs of If two parallel lines are intersected by a transversal then prove that the bisectors of any pair of Two parallel lines intersected by transversal prove-bisectors Of two interior angle forms Rectangle 2.2 Video - Parallel Lines cut by a Transversal Proving Theorem: Two parallel lines are cut by a transversal If two parallel lines are intersected by a transversal, prove that the bisectors of the inte... Angles Made by Two Parallel Lines Cut by a Transversal Two parallel lines l and\nm are intersected by a transversal p . Show that\nthe quadrilateral fo... If a transversal intersects two lines such that the bisectors of a pair of corresponding angles are Lesson 6.1 Prove Angles are Congruent Using Parallel Lines Using Parallel Lines If a transversal intersects two parallel lines, then the Alternate Interior Angles are equal.Lec-11

Conclusion

All things considered, it is clear that write-up shares enlightening facts pertaining to If Two Parallel Lines Are Intersected By A Transversal Then Prove That. Throughout the article, the journalist portrays extensive knowledge in the domain. Importantly, the explanation about this component stands out as exceptionally insightful. Whats more, the write-up does a great job in breaking down complex concepts in an comprehensible manner. Furthermore, the scribe offers actual cases that make the subject matter more tangible. A further characteristic that marks this document as special is the profound exploration of a range of aspects related to If Two Parallel Lines Are Intersected By A Transversal Then Prove That. The authors thoroughness assures that spectators receive a holistic view of the subject matter. Thanks for taking the time to this content. Should you have any questions, please do not hesitate to reach out to me using comments or email. I anticipate your comments. In wrapping up, if you want to explore further, highlighted below are a few related entries that are likely engaging:Wishing you a great reading experience!