In Question 4point C Is Called A Mid Point Of The Line Segment Ab।prove That Every Line Segment Has

By viagraultimate On Nov 9, 2024 Last updated

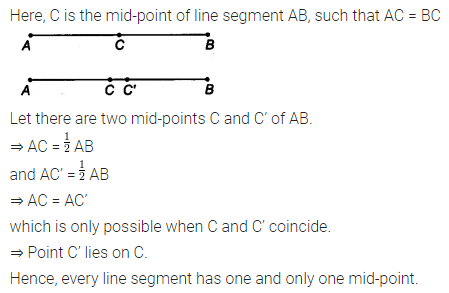
In Question 4 Point C Is Called A Mid Point Of Line Segment Ab Prove In question 4, point c is called a mid point of line segment ab. prove that every line segment has one and only one mid point. solution: we know that the things which coincide with one another are equal to one another. let us consider that line segment ab has two midpoints ‘c’ and ‘d’ as shown in the figure below. From equations (1) and (2), we get : ⇒ ac = ad. ⇒ c has to coincide with d for ac to be equal to ad. according to euclid's axiom 4: things which coincide with one another are equal to one another. hence, proved that a line segment has only one midpoint. answered by. 2 likes. in question 4, point c is called a mid point of line segment ab.

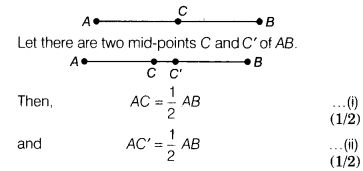
Point C Is Called A Mid Point Of Line Segment Ab Prove That Every Line Given: c is the mid point of ab such that ac = bc. to prove: ab has one and only mid point c. proof: suppose c and c' be the two mid points of ab. therefore ac = ab 2 and ac' = ab 2 => ac = ac' which is possible only when c and c' coincide => points c and c' are identical. hence, every line segment has one and only one mid point c. Ex 5.1, 5 in the above question, point c is called a mid point of line segment ab, prove that every line segment has one and only one mid point. in previous question, c was mid point of ab. Step by step video & image solution for in question 4, point 'c' is called a midpoint of line segment ab. prove that every line segment has one and only one mid point. by maths experts to help you in doubts & scoring excellent marks in class 9 exams. Let c and d are two mid points of line segment ab. according to question 4, we have, ac = 1 2 ab and ad = 1 2 ab ⇒ ac = ad [things which are equal to the same thing are equal to one another] it is possible only if c and d coincide with each other. hence, the mid point c is unique.

In Question 4 Point C Is Called A Mid Point Of Line Segment Ab Prove Step by step video & image solution for in question 4, point 'c' is called a midpoint of line segment ab. prove that every line segment has one and only one mid point. by maths experts to help you in doubts & scoring excellent marks in class 9 exams. Let c and d are two mid points of line segment ab. according to question 4, we have, ac = 1 2 ab and ad = 1 2 ab ⇒ ac = ad [things which are equal to the same thing are equal to one another] it is possible only if c and d coincide with each other. hence, the mid point c is unique. Let there be two such mid points c and d. then from above theorem ac = 1 2 ab and ad = 1 2 ab ∴ ac = ad but this is possible only if d coincides with c. therefore c is the unique mid point. proved. In the above question, point c is called a mid point of line segment ab, prove that every line segment has one and only one mid point.

Step into a realm of limitless possibilities with our blog. We understand that the online world can be overwhelming, with countless sources vying for your attention. That's why we stand out by providing well-researched, high-quality content that educates and entertains. Our blog covers a diverse range of interests, ensuring that there's something for everyone. From practical how-to guides to in-depth analyses and thought-provoking discussions, we're committed to providing you with valuable information that resonates with your passions and keeps you informed. But our blog is more than just a collection of articles. It's a community of like-minded individuals who come together to share thoughts, ideas, and experiences. We encourage you to engage with our content, leave comments, and connect with fellow readers who share your interests. Together, let's embark on a quest for continuous learning and personal growth.

In question 4,point C is called a mid point of the line Segment AB।Prove that every line Segment has

In question 4,point C is called a mid point of the line Segment AB।Prove that every line Segment has In Que 4 Point C Is Called A Midpoint | Prove That Every Line Segment Has One And Only One Midpoint Prove that every line segment has one & only one mid point In Question point C is called a mid-point of line segment AB. Prove that every line segment has o... A point C is called the midpoint of a line segment bar(AB) if | CLASS 9 | INTRODUCTION TO EUCLI... Point C is called mid point of line segment AB prove that every line segment has only one mid point Midpoint of a line segment Midpoint of a Line Segment #N/A Midpoint of a Line Segment Midpoint Formula The midpoint of a Line segment Mid-Point of a Line Segment - the Formula and How to Use it CBSE Class-9 Maths NCERT solution - Introduction to Euclid's Geometry - Exercise 5.1 - Problem 5 Midpoint of Line Segment Midpoint of a Line Segment Coordinate Geometry - Mid-point of a line segment : ExamSolutions Midpoint of a line segment Once you understand midpoint, You can solve Midpoint and length of a line segment PREVIEW | Year 9 Mathematics | MaffsGuru.com

Conclusion

Upon a thorough analysis, it is evident that the publication shares helpful data concerning In Question 4point C Is Called A Mid Point Of The Line Segment Ab।prove That Every Line Segment Has. In the complete article, the journalist demonstrates remarkable understanding on the subject. Notably, the review of this component stands out as a key takeaway. Also, the publication is remarkable in deconstructing complex concepts in an digestible manner. On top of that, the creator contains real-world cases that amplify the engagement. Another aspect that makes this publication unique is the comprehensive analysis of a variety of aspects related to In Question 4point C Is Called A Mid Point Of The Line Segment Ab।prove That Every Line Segment Has. The creators precise method guarantees that spectators receive a holistic view of the subject matter. Thank you for delving into the write-up. If you need further information, please feel free to send an email over social media platforms. I am enthusiastic about your messages. In summing up, to continue your journey, below are multiple similar essays that are potentially insightful:Wishing you enjoyable reading!