Inscribed Triangle

How To Find The Area Of A Right Triangle Inscribed In A Circle At In the first two cases, draw a perpendicular line segment from o to ¯ ab at the point d. figure 2.5.2 circumscribed circle for abc. the radii ¯ oa and ¯ ob have the same length r, so aob is an isosceles triangle. thus, from elementary geometry we know that ¯ od bisects both the angle ∠aob and the side ¯ ab. A circle is inscribed in the triangle if the triangle's three sides are all tangents to a circle. in this situation, the circle is called an inscribed circle, and its center is called the inner center, or incenter. imgur.
All 98 Images The Shortest Distance From The Center Of The Inscribed In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches (is tangent to) the three sides. the center of the incircle is a triangle center called the triangle's incenter. [1]. Learn what a triangle inside a circle (or circumscribed triangle) is, and explore its properties, theorems, and formulas. see examples of how to find the radius, area, and angles of a triangle inside a circle. Learn how to find missing side lengths of a right triangle with a line through the middle using pythagorean theorem and similar triangles. follow six steps with examples and tips to solve inscribed triangles problems. How to inscribe a circle in a triangle. using just a compass and a straightedge. inscribe: to draw on the inside of, just touching but never crossing the sides (in this case the sides of the triangle). steps: bisect one of the angles. bisect another angle. where they cross is the center of the inscribed circle, called the incenter.
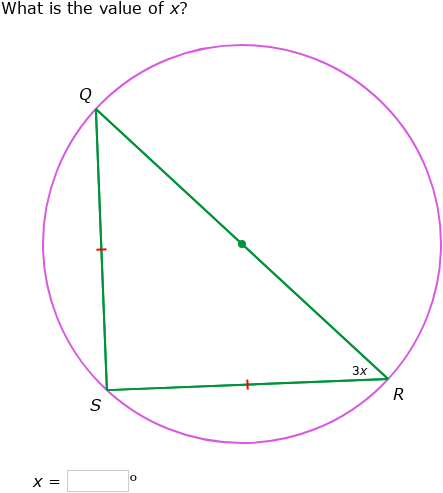
Ixl Angles In Inscribed Right Triangles Year 10 Maths Practice Learn how to find missing side lengths of a right triangle with a line through the middle using pythagorean theorem and similar triangles. follow six steps with examples and tips to solve inscribed triangles problems. How to inscribe a circle in a triangle. using just a compass and a straightedge. inscribe: to draw on the inside of, just touching but never crossing the sides (in this case the sides of the triangle). steps: bisect one of the angles. bisect another angle. where they cross is the center of the inscribed circle, called the incenter. The circumscribed circle of a triangle is centered at the circumcenter, which is where the perpendicular bisectors of all three sides meet each other. in contrast, the inscribed circle of a triangle is centered at the incenter, which is where the angle bisectors of all three angles meet each other. In geometry, an inscribed angle is the angle formed in the interior of a circle when two chords intersect on the circle. it can also be defined as the angle subtended at a point on the circle by two given points on the circle. equivalently, an inscribed angle is defined by two chords of the circle sharing an endpoint.

Comments are closed.