Integrated Rate Equation For First Order Reaction First Order

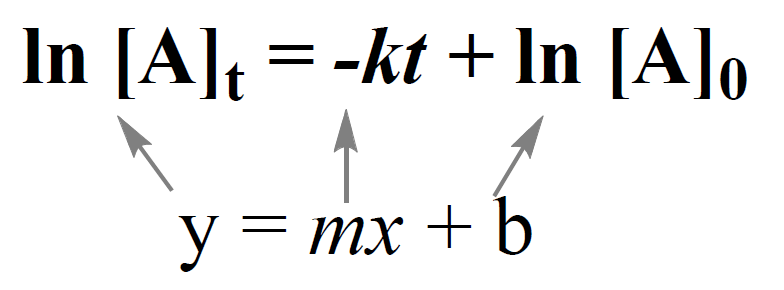
Integrated Rate Law Chemistry Steps The exponential form of the integrated rate law for a first order reaction (equation \(\ref{14.4.6}\)) is [a] = [a] 0 e −kt. a having been given the initial concentration of ethyl chloride ([a] 0) and having the rate constant of k = 1.6 × 10 −6 s −1, we can use the rate law to calculate the concentration of the reactant at a given time t. For zero order reactions, the differential rate law is: rate = k[a]0 = k. a zero order reaction thus exhibits a constant reaction rate, regardless of the concentration of its reactants. the integrated rate law for a zero order reaction also has the form of the equation of a straight line: [a] = − kt [a]0 y = mx b.

The First Order Integrated Rate Law And Half Life Part 4 Youtube Example of first order reaction. an example of a first order reaction is the hydrogenation of ethene. c 2 h 4 h 2 → c 2 h 6. therefore the rate of reaction for the above is k [c 2 h 4]. hence, equations iii and vii are the equations of rate constants of zero and first order reactions respectively. Example 12.4.3: the integrated rate law for a second order reaction. the reaction of butadiene gas (c 4 h 6) to yield c 8 h 12 gas is described by the equation: 2c4h6(g) c8h12(g) this “dimerization” reaction is second order with a rate constant equal to 5.76 10 −2 l mol −1 min −1 under certain conditions. The integrated rate law for second order reactions has the form of the equation of a straight line: 1 [a]t = kt 1 [a] 0 y = mx b. a plot of 1 [a]t versus t for a second order reaction is a straight line with a slope of k and a y intercept of 1 [a] 0. if the plot is not a straight line, then the reaction is not second order. The integrated rate law for a zero order reaction also has the form of the equation of a straight line: [a]t = −kt [a]0 y = mx b [a] t = − k t [a] 0 y = m x b. as shown in figure 18.4.6, a plot of [a] versus t for a zero order reaction is a straight line with a slope of − k and a y intercept of [a] 0. figure 18.4.6.

Integrated Rate Equation For First Order Reaction First Order The integrated rate law for second order reactions has the form of the equation of a straight line: 1 [a]t = kt 1 [a] 0 y = mx b. a plot of 1 [a]t versus t for a second order reaction is a straight line with a slope of k and a y intercept of 1 [a] 0. if the plot is not a straight line, then the reaction is not second order. The integrated rate law for a zero order reaction also has the form of the equation of a straight line: [a]t = −kt [a]0 y = mx b [a] t = − k t [a] 0 y = m x b. as shown in figure 18.4.6, a plot of [a] versus t for a zero order reaction is a straight line with a slope of − k and a y intercept of [a] 0. figure 18.4.6. The common integrated rate laws. for a zero order reaction: a products , rate = k. the integrated rate law is [a] = kt [a o] for a first order reaction: a products , rate = k [a] the integrated rate law is ln [a] = kt ln [a o] for a second order reaction: 2a products or a b products (when [a] = [b]) , rate = k [a] 2. Integration of the rate law for a simple first order reaction $(rate=k[a])$ results in an equation describing how the reactant concentration varies with time: $$ ln(\frac{[a] 0}{ [a] t })=kt \label{eq1}\tag{1}$$ where k is the rate constant, the initial concentration is [a] 0 and [a] t is the concentration present after any given time t. this.

What Is Integrated Rate Law For First Order Gas Reaction The common integrated rate laws. for a zero order reaction: a products , rate = k. the integrated rate law is [a] = kt [a o] for a first order reaction: a products , rate = k [a] the integrated rate law is ln [a] = kt ln [a o] for a second order reaction: 2a products or a b products (when [a] = [b]) , rate = k [a] 2. Integration of the rate law for a simple first order reaction $(rate=k[a])$ results in an equation describing how the reactant concentration varies with time: $$ ln(\frac{[a] 0}{ [a] t })=kt \label{eq1}\tag{1}$$ where k is the rate constant, the initial concentration is [a] 0 and [a] t is the concentration present after any given time t. this.