Interior Angle Measures Of Polygons

Interior Angles Of Polygons Mr Mathematics If it is a regular polygon (all sides are equal, all angles are equal) shape sides sum of interior angles shape each angle; triangle: 3: 180° 60° quadrilateral: 4: 360° 90° pentagon: 5: 540° 108° hexagon: 6: 720° 120° heptagon (or septagon) 7: 900° 128.57 ° octagon: 8: 1080° 135° nonagon: 9: 1260° 140° any polygon: n (n−2. Method 1: if “n” is the number of sides of a polygon, then the formula is given below: interior angles of a regular polygon = [180° (n) – 360°] n. method 2: if the exterior angle of a polygon is given, then the formula to find the interior angle is. interior angle of a polygon = 180° – exterior angle of a polygon.

Interior Angles Of Regular Polygons A Plus Topper What is the sum of the interior angles of a polygon? the sum of the interior angles of a polygon of n sides can be calculated with the formula 180(n 2)°. it helps us in finding the total sum of all the angles of a polygon, whether it is a regular polygon or an irregular polygon. by using this formula, we can verify the angle sum property as. If the shape is not regular then you can’t assume all of the angles are congruent. let’s look at an example with non regular interior angles. if the shape is not regular then you can’t assume all of the angles are congruent. 1 5 8 9 = 125^\circ 82^\circ 3x 39^\circ 6x 6^\circ =360^\circ. power series multiplication to find the product. Interior angle = 120° solve. so, the measure of each interior angle of the board is 120°. example 3: find the sum of the interior angles of a polygon with five sides. solution: given n = 5. s = (n – 2) x 180° formula for the sum of interior angles of polygon. s = (5 – 2) x 180° substitute 5 for n. s = 540°. How to solve problems involving interior angles of a polygon. in order to solve problems involving interior angles of a polygon: identify the number of sides in any polygon given in the question. note whether the shape is regular or irregular. find the sum of interior angles of the polygon(s) given. identify what the question is asking.

Interior Angles Of A Polygon Gcse Maths Steps Examples Interior angle = 120° solve. so, the measure of each interior angle of the board is 120°. example 3: find the sum of the interior angles of a polygon with five sides. solution: given n = 5. s = (n – 2) x 180° formula for the sum of interior angles of polygon. s = (5 – 2) x 180° substitute 5 for n. s = 540°. How to solve problems involving interior angles of a polygon. in order to solve problems involving interior angles of a polygon: identify the number of sides in any polygon given in the question. note whether the shape is regular or irregular. find the sum of interior angles of the polygon(s) given. identify what the question is asking. In order to find the measure of a single interior angle of a regular polygon (a polygon with sides of equal length and angles of equal measure) with n sides, we calculate the sum interior anglesor $$ (\red n 2) \cdot 180 $$ and then divide that sum by the number of sides or $$ \red n$$. Since all the interior angles of a regular polygon are equal, each interior angle can be calculated by dividing the sum of the angles by the number of sides. each interior angle of a regular polygon $= \frac{180^\circ \times (n\; \;2)}{n}$ let us use this formula to calculate the interior angle of a regular hexagon.
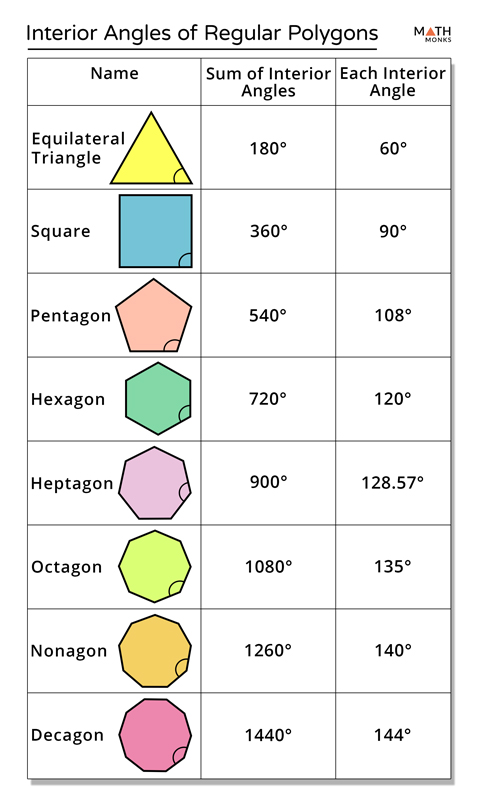
Regular Polygons Chart In order to find the measure of a single interior angle of a regular polygon (a polygon with sides of equal length and angles of equal measure) with n sides, we calculate the sum interior anglesor $$ (\red n 2) \cdot 180 $$ and then divide that sum by the number of sides or $$ \red n$$. Since all the interior angles of a regular polygon are equal, each interior angle can be calculated by dividing the sum of the angles by the number of sides. each interior angle of a regular polygon $= \frac{180^\circ \times (n\; \;2)}{n}$ let us use this formula to calculate the interior angle of a regular hexagon.
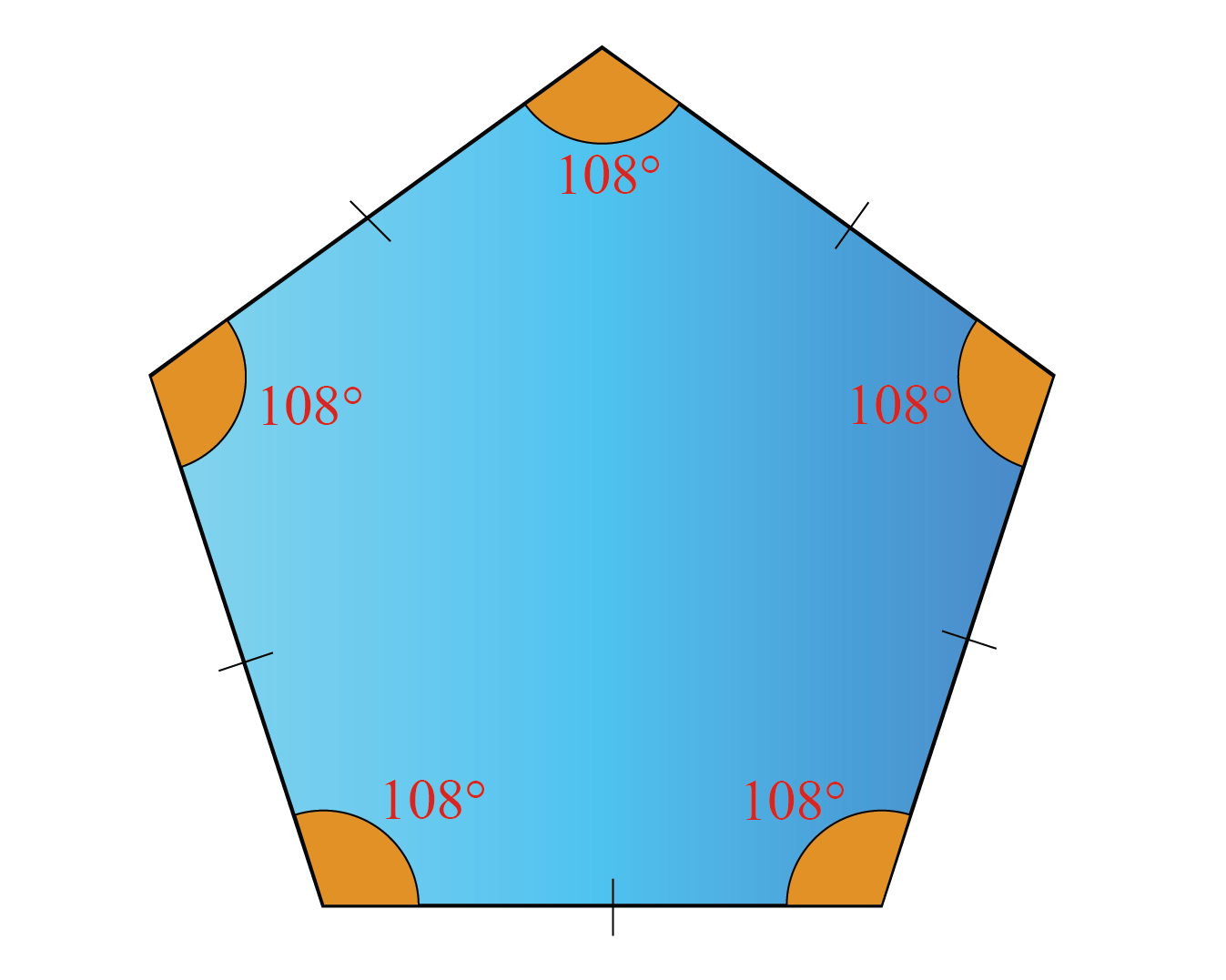
Interior Angles Solved Examples Geometry Cuemath

Comments are closed.