Intro To Derivative Notes Intro To The Derivative Tangent Line

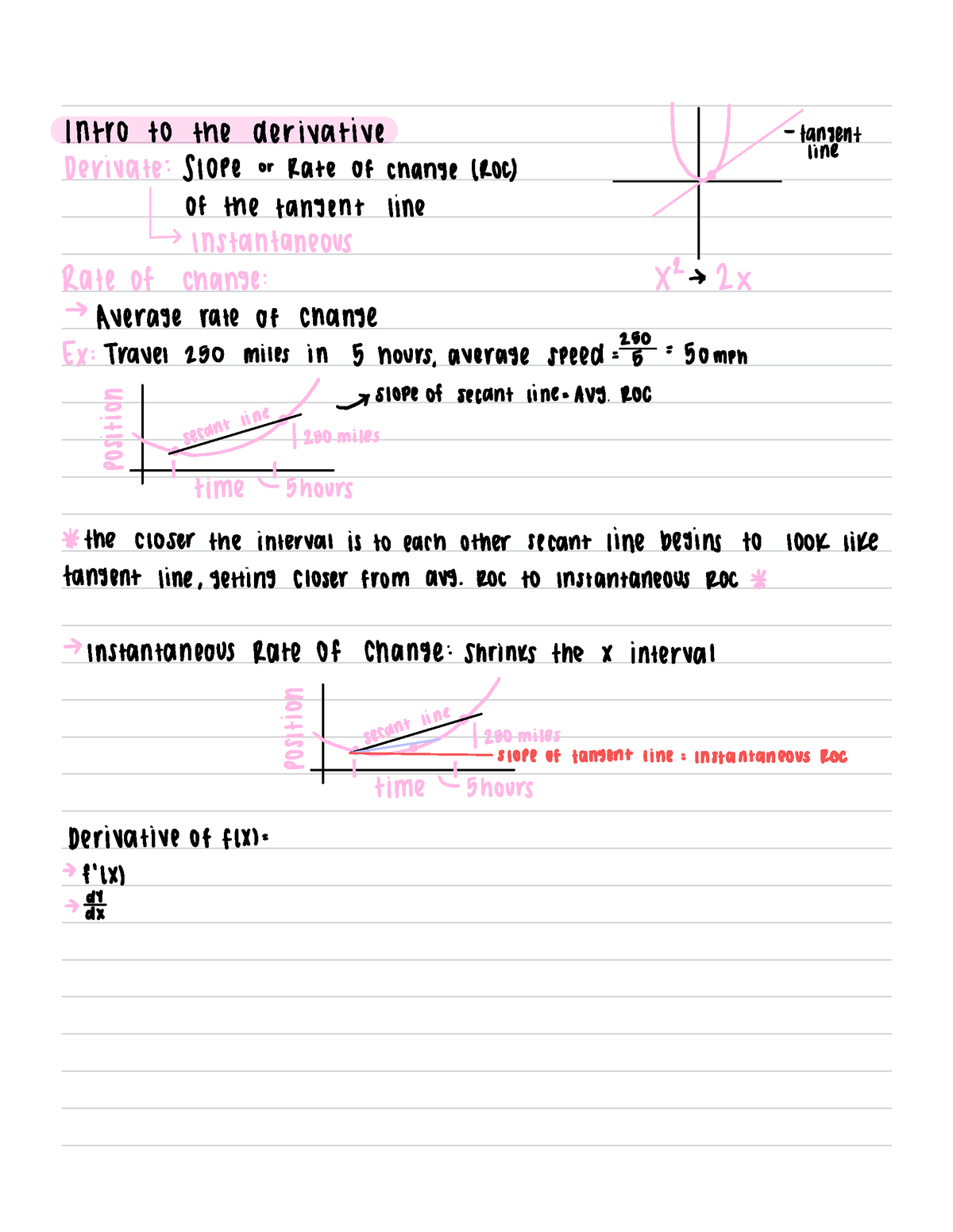
Intro To Derivative Notes Intro To The Derivative Tangent Line The derivative of a function describes the function's instantaneous rate of change at a certain point. another common interpretation is that the derivative gives us the slope of the line tangent to the function's graph at that point. learn how we define the derivative using limits. learn about a bunch of very useful rules (like the power, product, and quotient rules) that help us find. Definition: derivative function. let f be a function. the derivative function, denoted by f ′, is the function whose domain consists of those values of x such that the following limit exists: f ′ (x) = lim h → 0f(x h) − f(x) h. a function f(x) is said to be differentiable at a if f ′ (a) exists.

2 1a The Slope Of A Tangent Line Intro To Derivatives Youtube Learn about derivatives as the instantaneous rate of change and the slope of the tangent line. this video introduces key concepts, including the difference between average and instantaneous rates of change, and how derivatives are central to differential calculus. master various notations used to represent derivatives, such as leibniz's, lagrange's, and newton's notations. The slope of a curve at a point. "slope" is a concept that can easily be applied to linear functions. it is the change in y divided by the change in x. to calculate the slope of a line, we pick any two points on that line and divide the difference in their y values by the difference in their x values. introduction to derivatives quizzes. Historically, the primary motivation for the study of differentiation was the tangent line problem, which is the task of, for a given curve, finding the slope of the straight line that is tangent to that curve at a given point. the word tangent comes from the latin word tangens, which means touching. thus, to solve the tangent line problem, we. Derivatives: notes, rules, and examples 1) constant the derivative of a constant is zero; that is, for a constant c: 0 example: 2) scalar multiple 6 o (c) (slope at any point on the is 0) cx c the derivative of a constant multiplied by a ftnction is the constant multiplied by the derivative of the original function: (2 parallel lines the.

Intro To Derivatives Limits Tangent Lines In Calculus Step By Step Historically, the primary motivation for the study of differentiation was the tangent line problem, which is the task of, for a given curve, finding the slope of the straight line that is tangent to that curve at a given point. the word tangent comes from the latin word tangens, which means touching. thus, to solve the tangent line problem, we. Derivatives: notes, rules, and examples 1) constant the derivative of a constant is zero; that is, for a constant c: 0 example: 2) scalar multiple 6 o (c) (slope at any point on the is 0) cx c the derivative of a constant multiplied by a ftnction is the constant multiplied by the derivative of the original function: (2 parallel lines the. This session provides a brief overview of unit 1 and describes the derivative as the slope of a tangent line. it concludes by stating the main formula defining the derivative. lecture videos and notes video excerpts. clip 1: introduction to 18.01; clip 2: geometric interpretation of differentiation; clip 3: limit of secants; clip 4: slope as ratio. Derivatives of all six trig functions are given and we show the derivation of the derivative of sin(x) sin. ⁡. (x) and tan(x) tan (x). derivatives of exponential and logarithm functions – in this section we derive the formulas for the derivatives of the exponential and logarithm functions. derivatives of inverse trig functions – in this.

The Derivatives Notes 1 Derivatives And Differentiation The Tangent This session provides a brief overview of unit 1 and describes the derivative as the slope of a tangent line. it concludes by stating the main formula defining the derivative. lecture videos and notes video excerpts. clip 1: introduction to 18.01; clip 2: geometric interpretation of differentiation; clip 3: limit of secants; clip 4: slope as ratio. Derivatives of all six trig functions are given and we show the derivation of the derivative of sin(x) sin. ⁡. (x) and tan(x) tan (x). derivatives of exponential and logarithm functions – in this section we derive the formulas for the derivatives of the exponential and logarithm functions. derivatives of inverse trig functions – in this.

The Derivative Tangent Line Equations Derivatives Introduction Ap

Pre Calculus H Section 10 2 Notes Intro To Tangent Lines Derivatives