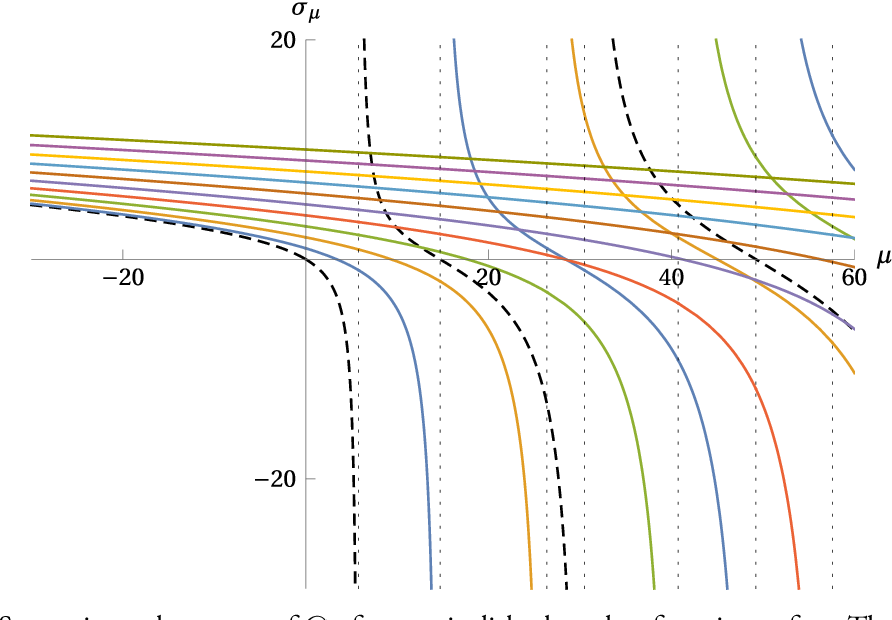
Figure 1 From The Dirichlet To Neumann Map The Boundary Laplacian And Alexandre girouard, mikhail karpukhin, michael levitin, iosif polterovich, the dirichlet to neumann map, the boundary laplacian, and hörmander’s rediscovered manuscript. j. spectr. theory 12 (2022), no. 1, pp. 195–225. doi 10.4171 jst 399. How close is the dirichlet to neumann (dtn) map to the square root of the corresponding boundary laplacian? this question has been actively investigated in recent years. somewhat surprisingly, a lot of techniques involved can be traced back to a newly rediscovered manuscript of hörmander from the 1950s. we present hörmander's approach and its applications, with an emphasis on eigenvalue.
Iosif Polterovich The Dirichlet To Neumann Map The Boundary Laplacian §1.2. the dirichlet to neumann map and the boundary laplacian. the goal of this paper is to explore the links between the dirichlet to neumann map d and the boundary laplacian ¢m. if ›has a smooth boundary m, d is a self adjoint elliptic pseudodi˘erential operator of order one on m with the same principal symbol as p. The dirichlet to neumann map, the boundary laplacian, and hörmander’s rediscovered manuscript alexandre girouard, mikhail karpukhin, michael levitin, and iosif polterovich abstract. how close is the dirichlet to neumann (dtn) map to the square root of the cor responding boundary laplacian? this question has been actively investigated in. 1.1 the steklov spectrum and the dirichlet to neumann map; 1.2 the dirichlet to neumann map and the boundary laplacian; 1.3 hörmander’s identity and its applications; 1.4 plan of the paper; acknowledgements; 2 commutators and rigidity. 2.1 proof of theorem 1.3; 2.2 discussion and open problems; 3 the proofs of hörmander’s identity and its. Alexander girouard, mikhail karpukhin, michael levitin and iosif polterovich, the dirichlet to neumann map, the boundary laplacian and hörmander's rediscovered manuscript, j. spectral theory 12 (2022), no. 1, 195 225.
Illustration Of The Boundary Layers For Dirichlet Neumann And Mixed 1.1 the steklov spectrum and the dirichlet to neumann map; 1.2 the dirichlet to neumann map and the boundary laplacian; 1.3 hörmander’s identity and its applications; 1.4 plan of the paper; acknowledgements; 2 commutators and rigidity. 2.1 proof of theorem 1.3; 2.2 discussion and open problems; 3 the proofs of hörmander’s identity and its. Alexander girouard, mikhail karpukhin, michael levitin and iosif polterovich, the dirichlet to neumann map, the boundary laplacian and hörmander's rediscovered manuscript, j. spectral theory 12 (2022), no. 1, 195 225. We show that the full symbol of the dirichlet to neumann map of the k form laplace's equation on a riemannian manifold (of dimension greater than 2) with boundary determines the full taylor series. • special to this example: girouard, karpukhin, levitin and polterovich [109] showed that euclidean balls are the only compact riemannian manifolds for which the dirichlet to neumann operator.
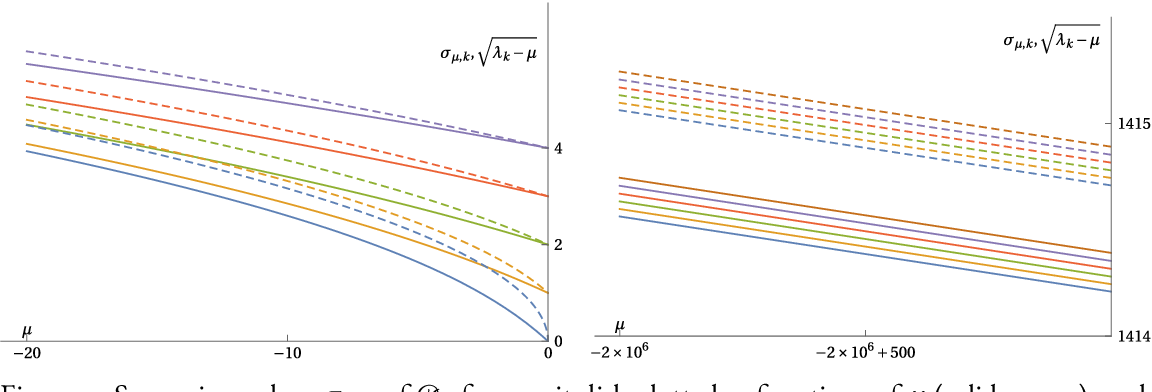
Figure 2 From The Dirichlet To Neumann Map The Boundary Laplacian And We show that the full symbol of the dirichlet to neumann map of the k form laplace's equation on a riemannian manifold (of dimension greater than 2) with boundary determines the full taylor series. • special to this example: girouard, karpukhin, levitin and polterovich [109] showed that euclidean balls are the only compact riemannian manifolds for which the dirichlet to neumann operator.
Comments are closed.