Matematica Funcao Exponencial

Função Exponencial Gráfico E Exemplos Infinittus Função exponencial é aquela que a variável está no expoente e cuja base é sempre maior que zero e diferente de um. essas restrições são necessárias, pois 1 elevado a qualquer número resulta em 1. assim, em vez de exponencial, estaríamos diante de uma função constante. além disso, a base não pode ser negativa, nem igual a zero. Aprenda o que é uma função exponencial, bem como conheça seus tipos e como seu gráfico é construído. veja ainda exercícios resolvidos sobre o tema!.

Função Exponencial Gráfico E Exemplos Infinittus 4ª propriedade. o gráfico da função exponencial nunca corta o eixo x. por menor que seja o valor da imagem, ele nunca chegará a ser 0. dizemos que ele tende a 0, mas não existe valor de x que faça com que f (x) = 0. conheça mais detalhes sobre essas propriedades, acessando o texto: propriedades da função exponencial. A função exponencial é a função f : r → r * , definida como f(x) = a x, com 0 < a ≠ 1. ou seja, a função possui domínio em r e imagem em r * que o conjunto dos números reais positivos e sem o zero. gráfico da função exponencial. podemos entender o gráfico de uma função do tipo exponencial aplicando valores ao expoente dela. A função exponencial é aquela que possui a variável (x) no expoente de uma potência cuja base é um número constante maior que zero e diferente de 1. ex: na função f (x) = 3 ˣ , temos que a base é igual a 3 e podemos descobrir valores para f (x) apenas substituindo o valor de x no expoente: podemos observar que conforme x cresce, f (x. Quando uma matéria é radioativa, é comum que a sua massa se desintegre, no decorrer do tempo, de forma exponencial. o césio 137, por exemplo, possui meia vida após 30 anos, ou seja, se havia, inicialmente, uma massa m 0 de césio, após 30 anos, haverá metade de m 0. para descrever melhor essa situação, temos a função exponencial:.
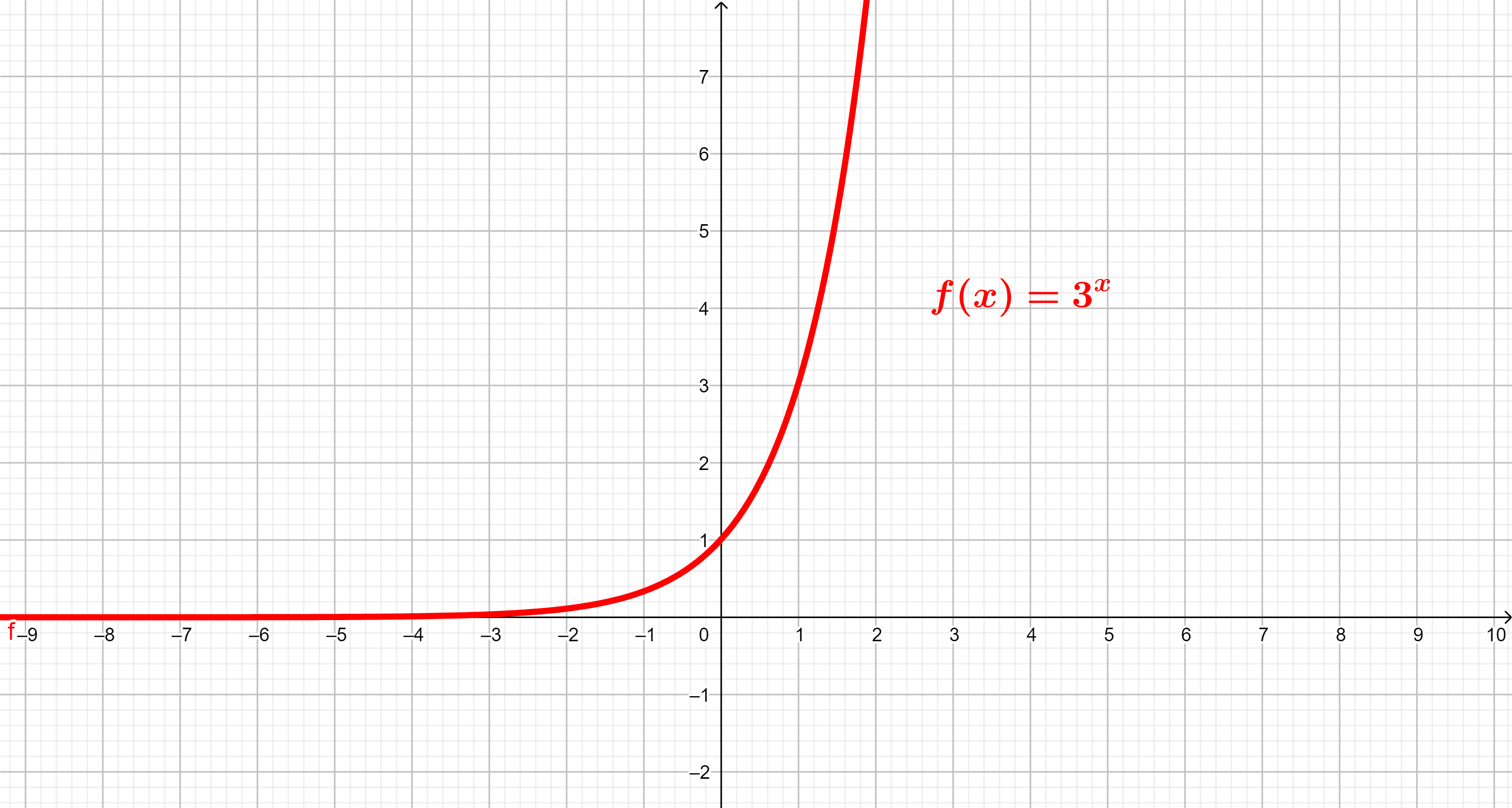
Função Exponencial O Que é Resumo Características Gráfico Curva A função exponencial é aquela que possui a variável (x) no expoente de uma potência cuja base é um número constante maior que zero e diferente de 1. ex: na função f (x) = 3 ˣ , temos que a base é igual a 3 e podemos descobrir valores para f (x) apenas substituindo o valor de x no expoente: podemos observar que conforme x cresce, f (x. Quando uma matéria é radioativa, é comum que a sua massa se desintegre, no decorrer do tempo, de forma exponencial. o césio 137, por exemplo, possui meia vida após 30 anos, ou seja, se havia, inicialmente, uma massa m 0 de césio, após 30 anos, haverá metade de m 0. para descrever melhor essa situação, temos a função exponencial:. Professor de matemática e física. a função exponencial é toda função de ℝ em ℝ * , definida por f (x) = a x, onde a é um número real, maior que zero e diferente de 1. aproveite os exercícios comentados para tirar todas as suas dúvidas sobre esse conteúdo e não deixe de verificar seus conhecimentos nas questões resolvidas de. A função exponencial é uma função com domínio e contradomínio no conjunto dos números reais e em que, na sua lei de formação, existe uma variável no expoente. descrevemos uma função exponencial como f: r → r, com a lei de formação f (x) = ax. em sua lei de formação, existem restrições para o valor da base a: ela sempre.
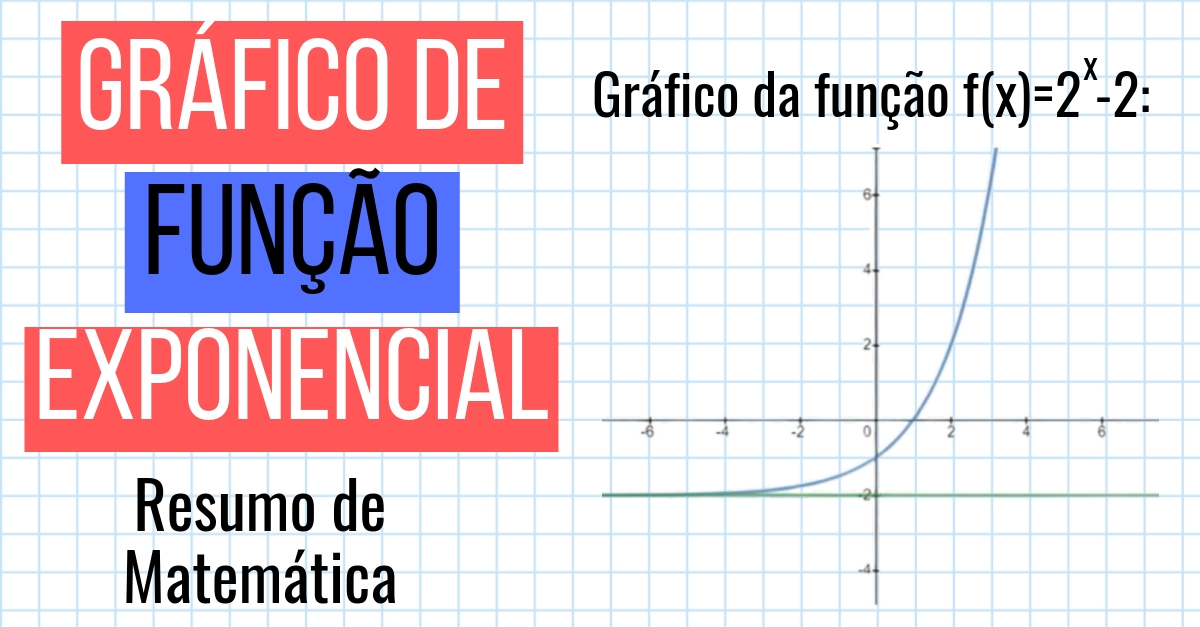
Gráfico De Função Exponencial Resumo De Matemática Professor de matemática e física. a função exponencial é toda função de ℝ em ℝ * , definida por f (x) = a x, onde a é um número real, maior que zero e diferente de 1. aproveite os exercícios comentados para tirar todas as suas dúvidas sobre esse conteúdo e não deixe de verificar seus conhecimentos nas questões resolvidas de. A função exponencial é uma função com domínio e contradomínio no conjunto dos números reais e em que, na sua lei de formação, existe uma variável no expoente. descrevemos uma função exponencial como f: r → r, com a lei de formação f (x) = ax. em sua lei de formação, existem restrições para o valor da base a: ela sempre.
Função Exponencial Toda Matéria

Função Exponencial Resumo De Função Exponencial Para Ensino Médio E

Comments are closed.